|
|
Savoir. La fabrique de l'ignorance. |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Posté le : 01/06/2021 17:18
|
|
|
|
|
Re: L. Ronald Hubbard |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Oui, c'est bien une secte, une des plus salement dangereuse car elle se revêt de l'apparence de la philosophie.
Posté le : 02/09/2017 18:11
|
|
|
|
|
Re: L. Ronald Hubbard |
|
Débutant  
Inscrit:
01/09/2017 15:13
De Castemaurou
Niveau : 1; EXP : 10
HP : 0 / 2
MP : 1 / 58
|
..Et accessoirement rappeler qu'il s'agit d'une véritable secte qui assèche financièrement et moralement ses adeptes...
Merci pour le partage
Tonnerre
Posté le : 01/09/2017 15:37
|
|
|
|
|
Re: Pierre Teilhard de Chardin |
|
Plume d'Or  
Inscrit:
18/02/2015 13:39
De Dijon
Niveau : 39; EXP : 1
HP : 190 / 950
MP : 767 / 27428
|
Bonsoir Lydia,
J'ai lu avec un grand intérêt l'article que tu nous proposes au sujet du Père Teilhard de Chardin. Je dois t'avouer que je suis très attaché à ses écrits.
Sois remerciée encore pour tous les articles que tu nous proposes. Ils nous éclairent et nous font grandir.
Bises.
Amitiés.
Jacques
Posté le : 03/06/2017 20:04
|
|
|
|
|
Lénonhard Euler |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Le 18 septembre 1783 meurt Leonhard Euler
à 76 ans à St Pétersbourg dans l'empire Russe, né le 15 avril 1707 à Bâle Suisse, mathématicien et physicien suisse, qui passa la plus grande partie de sa vie dans l'Empire russe et en Allemagne. Il était notamment membre de l'Académie royale des sciences de Prusse à Berlin.
Euler fit d'importantes découvertes dans des domaines aussi variés que le calcul infinitésimal et la théorie des graphes. Il introduisit également une grande partie de la terminologie et de la notation des mathématiques modernes, en particulier pour l'analyse mathématique, comme la notion de fonction mathématique. Il est aussi connu pour ses travaux en mécanique, en dynamique des fluides, en optique et en astronomie.
Euler est considéré comme un éminent mathématicien du XVIIIe siècle et l'un des plus grands et des plus prolifiques de tous les temps. Une déclaration attribuée à Pierre-Simon de Laplace exprime l'influence d'Euler sur les mathématiques : « Lisez Euler, lisez Euler, c'est notre maître à tous». Il était un fervent chrétien, croyant en l'inerrance biblique, et s'opposa avec force aux athées éminents de son temps.
En bref
Avec Joseph-Louis Lagrange, son émule plus jeune, Leonhard Paul Euler est l'un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d'une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique céleste et de la physique de son époque. Il a renouvelé l'articulation entre les secteurs mathématiques, fixé la plupart des notations du calcul infinitésimal que nous utilisons encore, développé la théorie des nombres de Fermat et systématisé la géométrie analytique de Descartes tout en l'étendant du plan à l'espace ; en mécanique et en élasticité, il a été le premier à pouvoir utiliser les développements contemporains de l'analyse (dont beaucoup lui étaient dus) en les conjuguant avec les principes de la physique newtonienne sur des bases théoriques solides.
Né à Bâle d'un père pasteur, Paul Euler (1670-1745), qui avait étudié les mathématiques avec Jacques Bernoulli, le jeune Leonhard Euler, que son père destinait au ministère religieux, reçut une éducation très complète en théologie, langues orientales, médecine, physique, astronomie et mathématiques ; il étudia cette dernière science avec Jean Bernoulli et se lia d'amitié avec les deux fils, Nicolas et Daniel, de son maître. En 1727, il fut attiré à Saint-Pétersbourg par Nicolas et Daniel Bernoulli, pour siéger à l'Académie que l'impératrice Catherine Ire venait de fonder en 1725 ; un poste lui était offert dans la section de médecine et de physiologie. En 1730, il obtenait un poste en philosophie naturelle ; après la mort de Nicolas et le départ pour Bâle de Daniel Bernoulli en 1733, Euler se trouvait le principal mathématicien à Saint-Pétersbourg : il était déjà connu pour de nombreux ouvrages, dont un avait été primé par l'Académie des sciences de Paris en 1724 (sur la théorie des marées, prix partagé avec C. Maclaurin et D. Bernoulli). La perte de son œil droit en 1735 ne diminua pas son intense activité scientifique. À l'appel de Frédéric II, il se rendit à Berlin en 1741 pour faire partie de l'Académie de cette ville ; il n'y fut pas estimé à sa juste valeur et préféra retourner à Saint-Pétersbourg en 1766, année où il ressentit les premiers symptômes de la cataracte qui devait lui ôter l'usage de son œil gauche, malgré une opération en 1771, et le rendre aveugle pour les douze dernières années de sa vie. Sa cécité ne l'empêcha pas de continuer à travailler et à rédiger des mémoires qu'il dictait à des personnes de son entourage. Il mourut subitement en 1783, laissant derrière lui une œuvre scientifique d'une ampleur inégalée, dont le catalogue (établi par G. Eneström en 1910-1913) ne comporte pas moins de 886 titres ; ses œuvres complètes comprennent près de quatre-vingts volumes. Christian Houzel
Sa vie
Leonhard Euler naquit à Bâle1 de Paul Euler, pasteur des Églises réformées et de Marguerite Brucker, fille de pasteur. Il eut deux jeunes sœurs du nom d'Anna Maria et de Maria Magdalena4. Peu de temps après la naissance de Leonhard, la famille Euler déménagea de Bâle pour rejoindre la ville voisine de Riehen, où Euler passa la plus grande partie de son enfance. Paul Euler était un ami de la famille Bernoulli — Jean Bernoulli, alors considéré comme le principal mathématicien européen, pourrait être celui ayant eu la plus grande influence sur le jeune Leonhard. L'éducation officielle d'Euler commença tôt à Bâle, où il fut envoyé vivre avec sa grand-mère maternelle. À l'âge de treize ans, il s'inscrivit à l'université de Bâle, et en 1723 obtint sa maîtrise de philosophie Magister Philosophiae, grâce à une dissertation qui comparait la philosophie de Descartes à celle de Newton. À cette époque, il recevait tous les samedis après-midi des leçons de Jean Bernoulli, qui découvrit rapidement chez son nouvel élève un incroyable talent pour les mathématiques5. Euler commença alors à étudier la théologie, le grec et l'hébreu à la demande de son père, afin de devenir pasteur, mais Jean Bernoulli convainquit Paul Euler que Leonhard était destiné à devenir un grand mathématicien. En 1727, il participa au concours de l'Académie des sciences de Paris qui consistait à résoudre un problème scientifique. Cette année-là, le problème était de trouver la meilleure façon de placer les mâts d'un navire. Euler remporta la deuxième place, derrière Pierre Bouguer, qui est maintenant connu comme le « père de l'architecture navale ». Par la suite, Euler gagna ce prestigieux prix annuel douze fois dans sa carrière.
Saint-Pétersbourg
À cette époque, les deux fils de Jean Bernoulli, Daniel et Nicolas, travaillaient à l'Académie des sciences de Russie à Saint-Pétersbourg. En juillet 1726, Nicolas mourut de l'appendicite, après avoir passé un an en Russie, et quand Daniel reprit les positions de son frère en mathématiques et en physique, il recommanda que le poste en physiologie qu'il avait laissé vacant fût comblé par son ami Leonhard Euler. En novembre 1726, Euler accepta l'offre avec empressement, mais fit le voyage à Saint-Pétersbourg avec retard, après avoir postulé en vain à un poste de professeur de physique à l'université de Bâle.
Euler arriva dans la capitale russe le 17 mai 1727. Occupant d'abord un poste au département médical de l'académie, il fut ensuite affecté au département de mathématiques. Il logeait auprès de Daniel Bernoulli, avec qui il travaillait souvent en étroite collaboration. Euler maîtrisait le russe et s'installa à Saint-Pétersbourg. Il prit également un emploi additionnel de médecin dans la marine russe.
Créée par Pierre le Grand, l'Académie de Saint-Pétersbourg était destinée à améliorer l'éducation en Russie et à combler le retard scientifique qui la séparait de l'Europe occidentale. En conséquence, elle était particulièrement intéressante pour les étudiants étrangers comme Euler. L'académie possédait suffisamment de ressources financières et une bibliothèque complète tirée de la bibliothèque privée de Pierre le Grand et de la noblesse russe. Très peu d'étudiants étaient inscrits dans l'Académie, de façon à diminuer la charge des professeurs, à mettre l'accent sur la recherche et à offrir à son corps professoral à la fois le temps et la liberté d'effectuer des recherches scientifiques.
Catherine Ire de Russie, qui poursuivait la politique de son défunt mari, décéda le jour de l'arrivée d'Euler. La noblesse russe prit alors le pouvoir lors de l'ascension de Pierre II de Russie, âgé de douze ans. La noblesse se méfiait des chercheurs étrangers ; elle réduisit le financement et causa d'autres difficultés à Euler et à ses collègues. Leurs conditions de travail s'améliorèrent légèrement à la mort de Pierre II ; Euler put donc rapidement gravir les échelons dans l'Académie, jusqu'à devenir professeur de physique en 1731. Deux ans plus tard, Daniel Bernoulli, lassé de la censure et de l'hostilité dont il faisait l'objet à Saint-Pétersbourg, partit pour Bâle. Euler lui succéda alors à la tête du département de mathématiques.
Le 7 janvier 1734, il épousa Katharina Gsell 1707-1773, fille du peintre Georg Gsell. Le jeune couple acheta une maison sur la Neva. De leurs treize enfants, cinq seulement atteignirent l'âge adulte13. Leonhard Euler, après le décès de Katharina Gsell en 1773, épouse l'année suivante une demi-sœur de celle-ci, Salomé Abigail Gsell 1723-1794, fille de Dorothea Graff 1678-1743 et de Georg Gsell 1673-1740. Dorothea Graff, fille de Maria Sibylla Merian était comme elle peintre et naturaliste, et avait accompagné sa mère dans ses expéditions au Surinam. Son mari, Georg Gsell, peintre et marchand d'art, recruté par Pierre le Grand en 1716, devint conservateur de la Kunstkamera).
Berlin
Préoccupé par la persistance des troubles en Russie, Euler quitta Saint-Pétersbourg le 19 juin 1741 pour occuper un poste à l'Académie de Berlin, qui lui était proposé par Frédéric II de Prusse. Il vécut pendant vingt-cinq ans à Berlin, où il écrivit plus de 380 articles. À Berlin, il publia deux célèbres ouvrages : l'Introductio in analysin infinitorum (« Introduction à l’analyse des infiniment petits »), un texte sur les fonctions publié en 1748 et Institutiones calculi differentialis (« Traité du calcul différentiel »), publié en 1755 et traitant du calcul différentiel.
En outre, Euler fut invité à être le professeur de la princesse d'Anhalt-Dessau, la nièce de Frédéric II. Euler lui écrivit plus de 200 lettres, qui furent ensuite rassemblées dans un best-seller intitulé Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie. Cet ouvrage contient des publications d'Euler sur divers sujets se rapportant à la physique et aux mathématiques, mais également sur des sujets philosophiques. Ce livre est devenu le plus largement lu de tous ses travaux mathématiques, et il a été publié en Europe et aux États-Unis. La popularité des « Lettres » témoigne de la capacité d'Euler à communiquer efficacement sur les questions scientifiques au public, une capacité rare pour un chercheur scientifique.
Malgré l'immense contribution d'Euler au prestige de l'Académie, il fut finalement contraint de quitter Berlin, en partie à cause d'un conflit de personnalité avec Frédéric II. En effet, le monarque avait moins de considération pour Euler que pour son cercle de philosophes. Voltaire faisait partie de ceux qui étaient aux côtés de Frédéric II, et il eut une bonne place dans le cercle du roi. Euler, simple homme religieux et travailleur acharné, était très classique dans ses convictions et ses goûts. Il fut, à bien des égards, l'opposé de Voltaire. Euler avait une formation limitée en rhétorique, et avait tendance à débattre sur des questions qu'il connaissait peu, faisant de lui une cible fréquente de l'esprit de Voltaire17. Frédéric II exprima également sa déception vis-à-vis des capacités d'ingénierie d'Euler :
Je voulais avoir un jet d'eau dans mon jardin : Euler a calculé la force des roues nécessaire afin d'élever l'eau jusqu'à un réservoir, d'où elle doit redescendre à travers des canaux, pour enfin sortir de la fontaine. Mon moulin a été réalisé géométriquement mais ne peut pas élever une goutte d'eau à moins de cinquante pas du réservoir. Vanité des vanités ! Vanité de la géométrie !
Déclin de la vue
Portrait de 1753 par Emanuel Handmann. Cette représentation indique des problèmes de la paupière droite et un possible strabisme. L'œil gauche semble en bonne santé, mais il a plus tard été affecté par une cataracte.
La vue d'Euler empira tout au long de sa carrière en mathématiques. Trois ans après avoir souffert d'une fièvre quasi mortelle en 1735, il devint presque aveugle de l'œil droit. Euler attribua plutôt son état au travail minutieux qu'il avait effectué en cartographie pour l'Académie de Saint-Pétersbourg. La vue d'Euler de l'œil droit empira tout au long de son séjour en Allemagne, si bien que Frédéric II le surnommait « Cyclope ». Euler souffrit ensuite d'une cataracte de l'œil gauche, le rendant presque totalement aveugle. Il semble que ce mauvais état ait eu peu d'effet sur sa productivité, Euler ayant compensé son handicap par ses compétences en calcul mental et par sa mémoire eidétique. Par exemple, Euler pouvait répéter l'Énéide de Virgile, du début à la fin, sans hésitation, et pour chaque page de son édition, il pouvait citer la première ligne et la dernière. Avec l'aide de ses scribes, la productivité d'Euler dans de nombreux domaines d'étude augmenta en fait. Ainsi, il produisit en moyenne un document de mathématiques par semaine au cours de l'année 1775.
Retour en Russie
La situation en Russie s'était grandement améliorée depuis l'accession au trône de Catherine II de Russie ; en 1766, Euler accepta une invitation à revenir à l'Académie de Saint-Pétersbourg. C'est ainsi qu'il passa le reste de sa vie en Russie. Son second séjour dans le pays fut cependant marqué par la tragédie. Un incendie à Saint-Pétersbourg en 1771 lui coûta son domicile, et faillit lui ôter la vie. En 1773, il perdit son épouse de 40 ans. Trois ans après la mort de sa femme, Euler se remaria avec la demi-sœur de celle-ci, Salomé Abigail Gsell (1723-1794). Ce mariage allait durer jusqu'à sa mort.
Le 18 septembre 1783, Euler décéda à Saint-Pétersbourg d'une hémorragie intra-cérébrale et fut enterré avec son épouse au cimetière luthérien de Smolensk sur l'île Vassilievski au XXe siècle le cimetière a été fermé, les restes d'Euler ont été transférés au cimetière Saint-Lazare du monastère Alexandre-Nevski). Son éloge funèbre fut écrit pour l'Académie française par le mathématicien et philosophe français Nicolas de Condorcet. Le récit de sa vie, avec une liste de ses œuvres, fut écrit par Nikolaus von Fuss, le beau-fils d'Euler et le secrétaire de l'Académie des sciences de Russie. Condorcet écrit dans son Éloge : « … il cessa de calculer et de vivre26 ».
Contributions aux mathématiques
Leonhard Euler a travaillé dans presque tous les domaines des mathématiques : la géométrie, le calcul infinitésimal, la trigonométrie, l'algèbre et la théorie des nombres. Il est une figure capitale de l'histoire des mathématiques : s'ils étaient imprimés, ses écrits, dont beaucoup sont d'un intérêt fondamental, pourraient occuper entre quarante et soixante ouvrages. Le nom d'Euler est associé à un grand nombre de sujets.
Notation mathématique
Euler a introduit et popularisé plusieurs conventions de notation par le biais de ses nombreux ouvrages largement diffusés. Plus particulièrement, il a introduit la notion de fonction2 et a été le premier à écrire f ( x ) {\displaystyle f(x)} pour désigner la fonction f {\displaystyle f} appliquée à l'argument x {\displaystyle x} , en 1734. Il a également introduit la notation moderne des fonctions trigonométriques, la lettre e pour la base du logarithme naturel également connue sous le nom de nombre d'Euler en 1727, la lettre grecque Σ pour désigner une somme en 175527 et la lettre i pour représenter l'unité imaginaire, en 1777. L'utilisation de la lettre grecque π pour désigner le rapport de la circonférence d'un cercle à son diamètre a également été popularisée par Euler, mais celui-ci n'est pas à l'origine de la notation.
Analyse
Le développement du calcul infinitésimal a été au premier plan des recherches mathématiques du XVIIIe siècle, et la famille Bernoulli — amis d'Euler — est à l'origine de nombreux progrès dans ce domaine. Grâce à leur influence, l'étude du calcul infinitésimal est devenu l'un des axes principaux du travail d'Euler. Bien que certaines des démonstrations d'Euler ne soient pas acceptables au regard des normes modernes de rigueur mathématique, ses idées ont tout de même conduit à de grandes avancées.
Euler est bien connu dans le domaine de l'analyse pour son usage fréquent des séries numériques et des séries entières. Il a notamment montré que le nombre e {\displaystyle \mathrm {e} } est la somme de la série de terme général 1 n ! {\displaystyle {\dfrac {1}{n\,!}}} :
e = ∑ n = 0 ∞ 1 n ! = lim n → ∞ ( 1 0 ! + 1 1 ! + 1 2 ! + ⋯ + 1 n ! ) ⋅ {\displaystyle \mathrm {e} =\sum _{n=0}^{\infty }{\dfrac {1}{n\,!}}=\lim _{n\to \infty }\left({\frac {1}{0\,!}}+{\frac {1}{1\,!}}+{\frac {1}{2\,!}}+\cdots +{\frac {1}{n\,!}}\right)\cdot }
Il a trouvé le « développement en série entière » de la fonction exponentielle :
e x = ∑ n = 0 ∞ x n n ! = lim n → ∞ ( 1 0 ! + x 1 ! + x 2 2 ! + ⋯ + x n n ! ) ⋅ {\displaystyle \mathrm {e} ^{x}=\sum _{n=0}^{\infty }{\dfrac {x^{n}}{n\,!}}=\lim _{n\to \infty }\left({\frac {1}{0\,!}}+{\frac {x}{1\,!}}+{\frac {x^{2}}{2\,!}}+\cdots +{\frac {x^{n}}{n\,!}}\right)\cdot }
et celui de la fonction arc tangente.
Sa ténacité à utiliser les développements en séries lui a permis de résoudre le fameux problème de Bâle en 1735 :
∑ n = 1 ∞ 1 n 2 = lim n → ∞ ( 1 1 2 + 1 2 2 + 1 3 2 + ⋯ + 1 n 2 ) = π 2 6 ⋅ {\displaystyle \sum _{n=1}^{\infty }{\dfrac {1}{n^{2}}}=\lim _{n\to \infty }\left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)={\frac {\pi ^{2}}{6}}\cdot }
Euler est pleinement conscient de la nécessité de démontrer rigoureusement les résultats de convergence dont il se sert, mais cela ne l'empêche pas d'écrire également des formules « paradoxales » telle que 1 + 2 + 4 + 8 + 16 + ⋯ = − 1 {\displaystyle 1+2+4+8+16+\dots =-1} , de définir des règles d'emploi et de calcul avec de telles séries divergentes, et de les utiliser pour obtenir des résultats inattendus concernant, par exemple, la fonction zêta.
Une interprétation géométrique de la formule d'Euler
Euler a introduit l'utilisation de la fonction exponentielle et des logarithmes dans les démonstrations en analyse. Il a découvert des moyens d'exprimer différentes fonctions logarithmiques en utilisant les séries entières, et il a étendu la notion de logarithme aux nombres négatifs et aux nombres complexes. Il a également défini la fonction exponentielle pour les nombres complexes, et a découvert la relation qui la lie aux fonctions trigonométriques :
pour tout réel φ {\displaystyle \varphi } , e i φ = cos ( φ ) + i sin ( φ ) . {\displaystyle \mathrm {e} ^{\,\mathrm {i} \,\varphi }=\cos(\varphi )+\mathrm {i} \,\sin(\varphi ).\,}
Un cas particulier de cette « formule d'Euler », obtenu en donnant à φ {\displaystyle \varphi } la valeur π {\displaystyle \pi } est
e i π = − 1 {\displaystyle \mathrm {e} ^{\,\mathrm {i} \,\pi }=-1\ } , qu'on préfère souvent écrire : e i π + 1 = 0 {\displaystyle \mathrm {e} ^{\,\mathrm {i} \,\pi }+1=0\,}
formule connue sous le nom d'identité d'Euler, et qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l'addition, la multiplication, l'exponentiation, l'égalité et les constantes remarquables 0, 1, e {\displaystyle \mathrm {e} } , i {\displaystyle \mathrm {i} } et π {\displaystyle \pi } . En 1988, les lecteurs de The Mathematical Intelligencer l'ont désignée comme « la plus belle formule mathématique de tous les temps ». Au total, le nom d'Euler figurait dans trois des cinq formules arrivées en tête de ce vote.
La formule de De Moivre
( cos ( x ) + i sin ( x ) ) n = cos ( n x ) + i sin ( n x ) {\displaystyle (\cos(x)+\mathrm {i} \,\sin(x))^{n}=\cos(nx)+\mathrm {i} \,\sin(nx)~}
est une conséquence directe de la formule d'Euler.
En outre, Euler a contribué à la théorie des fonctions transcendantes avec l'introduction de la fonction bêta et de la fonction gamma. Il a également introduit une nouvelle méthode pour résoudre les équations quartiques. Il a aussi trouvé une façon de calculer des intégrales avec des limites complexes, préfigurant le développement moderne de l'analyse complexe, et a inventé le calcul des variations, qui inclut l'un de ses résultats les plus célèbres, nommé l'équation d'Euler-Lagrange.
Euler fut le pionnier de l'utilisation de méthodes d'analyse pour résoudre des problèmes de la théorie des nombres. Ce faisant, il a réuni deux branches différentes des mathématiques et introduit un nouveau champ d'étude : la théorie analytique des nombres. Euler a aussi introduit la théorie des séries hypergéométriques, des fonctions hyperboliques et la théorie analytique des fractions continues. Par exemple, il a prouvé l'infinité des nombres premiers en utilisant la divergence de la série harmonique, et il a utilisé les méthodes analytiques pour avoir une meilleure compréhension de la répartition des nombres premiers. Les travaux d'Euler dans ce domaine ont contribué à l'élaboration du théorème des nombres premiers.
Théorie des nombres
L'intérêt d'Euler dans la théorie des nombres peut être attribué à l'influence de Christian Goldbach, son ami35 à l'Académie de Saint-Pétersbourg. Un grand nombre des premiers travaux d'Euler en théorie des nombres est fondé sur les travaux de Pierre de Fermat. Euler a développé quelques idées de Fermat, et a réfuté certaines de ses conjectures.
Euler a fait le lien entre la distribution des nombres premiers et l'analyse. Il a démontré que la série des inverses des nombres premiers diverge. Pour ce faire, il a découvert le lien entre la fonction zêta de Riemann et les nombres premiers.
Euler a démontré les identités de Newton, le petit théorème de Fermat, le théorème des deux carrés de Fermat, et il a également travaillé sur le théorème des quatre carrés de Lagrange. Il a aussi défini la fonction φ {\displaystyle \varphi } qui associe à tout entier n {\displaystyle n} le nombre d'entiers positifs inférieurs à n {\displaystyle n} et qui sont premiers avec n . {\displaystyle n.} En utilisant les propriétés de cette « indicatrice », il a généralisé le petit théorème de Fermat pour aboutir à ce qui est maintenant connu sous le nom de théorème d'Euler. Il a contribué de manière significative à la recherche sur les nombres parfaits, qui ont fasciné les mathématiciens depuis Euclide. Euler a également conjecturé la loi de réciprocité quadratique. Cet énoncé est considéré comme un théorème fondamental de la théorie des nombres, et en cela Euler a ouvert la voie aux travaux de Carl Friedrich Gauss.
En 1772, Euler a démontré que 2 31 − 1 = {\displaystyle 2^{31}-1=} 2 147 483 647 est un nombre de Mersenne premier. Il est resté le plus grand nombre premier connu jusqu'en 1867.
Géométrie
Comme dans les autres domaines des mathématiques, les contributions d'Euler à la géométrie sont exceptionnelles : angles d'Euler, droite d'Euler, cercle d'Euler, relation entre cercle inscrit et circonscrit, etc.
À titre d'exemple, il a montré que, pour tout triangle, les neuf points suivants :
les pieds des trois hauteurs H1 H2 H3 dans le diagramme
les milieux des trois côtés I1 I2 I3 dans le diagramme
les milieux de chacun des segments reliant l'orthocentre aux sommets du triangle J1 J2 J3 dans le diagramme
sont situés sur un même cercle39. Ce « cercle des neuf points » est encore appelé « cercle d'Euler » associé au triangle.
Il a démontré aussi que, dans tout triangle, l'orthocentre, le centre du cercle circonscrit, le centre de gravité et le centre du cercle des neuf points sont alignés. La droite qui les porte est appelée « droite d'Euler » associée au triangle.
Cercle et droite d'Euler d'un triangle quelconque
Théorie des graphes, Problème des sept ponts de Königsberg.
Carte de Königsberg au temps d'Euler, montrant le schéma réel de disposition des sept ponts
En 1736, Euler résolut le problème des sept ponts de Königsberg40. La ville de Königsberg, en Prusse, est traversée par la rivière Pregolia, qui entoure deux grandes îles reliées entre elles et aux deux rives par sept ponts. Le problème était de savoir s'il est possible de suivre un chemin qui emprunte chaque pont une fois et une seule et revienne au point de départ. Euler a établi que, pour que ce soit possible, il aurait fallu que chacune des quatre zones géographiques les deux îles et les deux rives soit atteinte par un nombre pair de ponts — en termes modernes : que chacun des quatre « sommets » du « graphe » soit adjacent à un nombre pair d'« arêtes » un graphe ayant cette propriété est dit « eulérien ». La résolution de ce problème est considérée comme le premier théorème de la théorie des graphes.
Euler a également établi la formule S − A + F = 2 {\displaystyle S-A+F=2} liant le nombre de sommets, d'arêtes et de faces d'un polyèdre convexe, et donc d'un graphe planaire. La constante de cette formule est maintenant connue comme la caractéristique d'Euler pour un graphe ou pour un autre objet mathématique, et est liée au genre de l'objet. L'étude et la généralisation de cette formule, notamment par Cauchy44 et L'Huillier45, est à l'origine de la topologie.
En outre, Leonhard Euler est le premier à avoir étudié le problème du cavalier, en 1759. Il publiera ses recherches sur la question dans Solution d'une question curieuse qui ne paraît soumise à aucune analyse.
Mathématiques appliquées
Certains des plus grands succès d'Euler ont été dans la résolution des problèmes analytiques dans des domaines autres que les mathématiques et dans la description de nombreuses applications des nombres de Bernoulli, des séries de Fourier, des diagrammes de Venn, des nombres d'Euler, des constantes e et π, des fractions continues et des intégrales. Il a développé des outils qui rendent plus faciles à appliquer certains problèmes physiques. Il a fait progresser le domaine de l'amélioration de l'approximation numérique d'intégrales, en inventant ce qui est maintenant connu sous le nom de méthode d'Euler. Euler a également démontré, en même temps que l'écossais Colin Maclaurin — mais bien indépendamment — la formule d'Euler-Maclaurin. Il a aussi facilité l'utilisation des équations différentielles, en particulier en introduisant la constante d'Euler-Mascheroni :
γ = lim n → ∞ ( 1 + 1 2 + 1 3 + 1 4 + ⋯ + 1 n − ln ( n ) ) . {\displaystyle \gamma =\lim _{n\rightarrow \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}-\ln(n)\right).
Un des domaines les moins communs qui intéressaient Euler était l'application des idées mathématiques à la musique. En 1739, il écrivit Tentamen novae theoriae musicae, dans l'espoir de finalement intégrer la théorie musicale aux mathématiques. Cette partie de son travail, cependant, n'a pas reçu une grande attention et a été décrite comme trop mathématique pour les musiciens mais aussi trop musicale pour les mathématiciens. On y trouve cependant le tout premier exemple de théorie des graphes avec une disposition des notes couramment utilisée de nos jours en analyse musicale, le Tonnetz, mieux développé dans De harmoniae veris principiis per speculum musicum repraesentatis en 1774.
Mathématiques
Euler est l'auteur de trois grands traités didactiques sur l'analyse infinitésimale, dans lesquels il a exposé sa conception nouvelle du calcul différentiel et intégral et ses rapports avec la géométrie : l'Introductio in analysin infinitorum (1748), les Institutiones calculi differentialis (1755) et les Institutiones calculi integralis (3 vol., 1768-1770). Le premier de ces traités opère une refonte dans le mode d'exposition de ces questions : il met au premier plan le concept de fonction, défini de façon formelle comme « une expression analytique composée d'une manière quelconque d'une quantité variable et de nombres ou de quantités constantes ». Cette définition reprend celle que Jean Bernoulli avait déjà donnée (le terme avait été introduit par Leibniz) ; l'originalité d'Euler tient dans le rôle fondamental qu'il fait jouer à ce concept, qui n'était que marginal avant lui. Le premier livre de l'Introductio est consacré au calcul « algébrique » sur les fonctions, étant entendu qu'Euler considère encore comme algébriques les procédures infinies qui étendent les opérations usuelles : séries et produits infinis, fractions continues ; au second livre, il applique les méthodes et les résultats du premier livre à des problèmes de géométrie (étude des courbes algébriques ou transcendantes, surfaces, changements d'axes de coordonnées). Il y a là un renversement très important par rapport aux traités antérieurs dans lesquels le calcul était au contraire tributaire de la géométrie. Euler donne dans l'Introductio ( chap. VI à VIII) un exposé des fonctions transcendantes élémentaires : la fonction exponentielle, le logarithme et les fonctions trigonométriques, qui sont envisagées ainsi pour la première fois. L'exponentielle az (où a > 0 est une constante) est définie par interpolation pour z réel, entre les valeurs rationnelles de z, et le logarithme est défini comme fonction inverse de l'exponentielle (ce qui est nouveau) ; les fonctions circulaires sin et cos sont, pour la première fois, considérées comme des fonctions d'une variable réelle (ou même complexe) et non plus comme des lignes qui dépendent d'un angle ; elles sont liées à l'exponentielle par les célèbres formules d'Euler :
où se trouvent le nombre e, base des logarithmes népériens (la notation e pour ce nombre est due à Euler, qui l'employait depuis 1728), et l'unité imaginaire − 1, notée ici i comme Euler l'a fait plus tard, en 1777. Un autre nombre célèbre, le rapport de la circonférence au diamètre, avait été noté π par W. Jones en 1706, mais c'est Euler qui a imposé cette notation à l'usage des mathématiciens ; il est lié aux précédents par la célèbre formule eiπ = − 1 écrite par Euler. Cette formule attribue le logarithme imaginaire iπ au nombre − 1, contrairement à ceux qui croyaient pouvoir déduire de l'égalité lg(− 1)2 = lg(+ 1)2 celle des logarithmes de 1 et de − 1. Le paradoxe précédent avait été résolu par Euler, qui avait montré que chaque nombre (réel ou complexe) a une infinité de logarithmes qui diffèrent entre eux par un multiple entier arbitraire de 2iπ ; dans le cas d'un nombre réel positif, un seul des logarithmes a une valeur réelle. À propos des logarithmes, Euler remarque que, lorsque a et b sont rationnels, lgab n'est ni rationnel (sauf si b est une puissance entière de a), ni la racine carrée d'un nombre rationnel ; c'est la base du septième problème de Hilbert, résolu en 1934 par Gelfond et Schneider (cf. HILBERT).
Euler était exceptionnellement doué pour le calcul, aussi bien numérique que formel. Dans l'Introductio, il manipule les séries et les produits infinis d'une façon prodigieuse et il trouve des résultats très remarquables, comme le développement de sin z en produit infini :
qui lui donne les sommes des séries :
sous la forme Anπ2n, avec An rationnel, dont Euler donne la valeur numérique pour 1 ≤ n ≤ 13. Le cas n = 1 était un problème célèbre, qui avait résisté à Jacques Bernoulli, et dont Euler avait communiqué la solution à D. Bernoulli vers 1736 ; dans le cas général, Euler a découvert plus tard le lien entre les coefficients An et les nombres de Bernoulli (Institutiones calculi differentialis, 2e part., chap. V). Il avait aussi calculé les valeurs numériques de :
pour 1 ≤ n ≤ 5, et leurs rapports respectifs à π2n+1, sans y reconnaître des nombres rationnels remarquables ; on sait depuis (Apéry, 1978) que ζ(3) est un nombre irrationnel, mais on n'en sait pas plus. Les nombres de Bernoulli apparaissent aussi dans la formule sommatoire découverte par Euler en 1732-1735 et, indépendamment, par Maclaurin, qui donne un développement asymptotique des sommes partielles d'une série ; pour la série harmonique :
qui est divergente et correspond à ζ(1), Euler trouve que :
est égal à lgn + γ + εn, où εn tend vers 0 pour n infini et γ = 0,577 215 664 9... est une constante connue sous le nom de constante d'Euler, dont on ne sait toujours pas si elle est rationnelle ou irrationnelle. Au chapitre XV de l'Introductio, Euler transforme la série ζ(s), s entier, en un produit infini faisant intervenir la suite des nombres premiers ; la divergence de ζ(1) lui donne alors non seulement l'infinitude des nombres premiers, mais encore la divergence de la série des inverses des nombres premiers, et même un équivalent lglgn pour la somme des n premiers termes de cette série. Ailleurs, il trouve une relation remarquable entre ζ(s) et la somme qu'il attribuait formellement à la série divergente ζ(1 − s) [s entier ≥ 2] ; cette équation fonctionnelle de la fonction zêta devait être démontrée au XIXe siècle, pour s complexe, par Malmsten, puis par Riemann qui en reconnut l'importance et fonda sur elle l'étude de la répartition des nombres premiers.
Euler avait découvert encore d'autres relations entre les produits ou les séries infinies et la théorie des nombres, par exemple à propos du problème des partitions d'entiers en sommes d'entiers (Introductio, chap. XVI) et du produit :
qu'il avait su transformer en une série entière dont les exposants sont les nombres pentagonaux.
D'autres contributions importantes d'Euler concernent le calcul intégral, comme la résolution générale des équations différentielles linéaires à coefficients constants, la formule d'addition pour les intégrales elliptiques, la découverte des intégrales appelées maintenant eulériennes, dont l'une réalise l'interpolation de n ! pour des valeurs non entières de n, l'étude de l'équation hypergéométrique et son intégration par une série entière, la résolution de nombreuses équations différentielles ou aux dérivées partielles par la méthode du facteur intégrant et les équations du calcul des variations. Comme d'Alembert l'avait reconnu à propos des cordes vibrantes en 1747, l'intégration d'une équation aux dérivées partielles fait intervenir des fonctions « arbitraires » (et non plus seulement des constantes arbitraires, comme pour les équations différentielles ordinaires) ; l'origine physique du problème conduisit Euler à prendre pour ces fonctions arbitraires des fonctions plus générales que celles de l'Introductio, définies par un graphe quelconque tracé à main libre, et non plus nécessairement par des expressions analytiques. Il s'ensuivit une controverse entre d'Alembert, Euler et D. Bernoulli, qui posa le problème du développement d'une fonction arbitraire en série trigonométrique ; une partie importante des recherches du XIXe siècle a tourné autour de ces questions.
À son époque, Euler était à peu près le seul à s'intéresser à la théorie des nombres. Tout au long de sa carrière, il a essayé de prouver les résultats laissés par Fermat sans démonstration : c'est ainsi qu'il démontra le petit théorème de Fermat, selon lequel ap-1 − 1 est divisible par p si p est un nombre premier et si a n'est pas divisible par p, et qu'il en trouva une généralisation. Pour le « dernier » théorème de Fermat, sur l'impossibilité de l'équation xn + yn = zn pour n ≥ 3, Euler donna une démonstration dans le cas de n = 3, en admettant pour les nombres complexes de la forme a + b− 3, avec a et b entiers, des propriétés arithmétiques analogues à celles des entiers ordinaires ; cela préfigure la théorie des entiers algébriques qui devait être développée au XIXe siècle par Kummer, Kronecker et Dedekind. On n'a toujours pas de démonstration valable du théorème pour n quelconque. Euler trouva une démonstration du fait que tout nombre premier de la forme 4n + 1 est somme de 2 carrés, mais laissa à Lagrange la gloire de démontrer que tout entier est somme de 4 carrés. Son habileté au calcul lui permit de trouver que 225 + 1 est divisible par 641, alors que Fermat avait conjecturé que 22n + 1 est toujours premier (c'est vrai pour 0 ≤ n ≤ 4, mais on ne connaît pas d'autre valeur de n pour laquelle ce serait encore vrai) ; il découvrit une soixantaine de paires de nombres amiables et démontra que les nombres parfaits pairs sont tous de la forme déjà connue d'Euclide : 2n-1(2n − 1), avec 2n − 1 premier (on ne sait toujours pas s'il existe des nombres parfaits impairs).
Euler s'était aussi posé des problèmes relevant de ce que l'on appelle maintenant la topologie : le problème des ponts de Königsberg et la relation (connue sous le nom de formule d'Euler) entre les nombres de sommets, d'arêtes et de faces d'un polyèdre convexe.
À côté de ses ouvrages de recherche, Euler publia aussi des livres d'enseignement assez élémentaires, comme sa célèbre Algèbre (publiée en russe en 1768) ; la traduction française a été complétée par des notes de Lagrange sur la théorie des nombres.
Mécanique, physique, astronomie
Euler a publié de nombreux ouvrages relatifs à la technique. En 1736, paraît son traité de mécanique, Mechanica sive motus scientia analytice exposita, où, pour la première fois, la mécanique du point matériel est conçue et exposée comme une science rationnelle. En 1765, il donnera sa Theoria motus corporum solidorum seu rigidorum, où il définit le centre d'inertie, les moments d'inertie et les axes principaux d'inertie, tandis qu'il intègre les équations du mouvement d'un solide de révolution autour d'un point fixe de l'axe ; son fils publiera, en 1790, une édition revue et augmentée de cet ouvrage.
Son traité de 1744, Methodus inveniendi lineas curvas maximi minimive proprietate gaudens, fonde le calcul des variations, dans la lignée des travaux de Jacques et Jean Bernoulli (l'ouvrage aura sur Lagrange une influence considérable). Un important appendice sur la détermination, par ce type de calcul, du mouvement d'un projectile dans un milieu résistant lui permet de justifier a posteriori le principe de la moindre action, de son ami P.-L. Maupertuis. Citons enfin, dans le domaine de la mécanique, ses études sur les cordes vibrantes ; les discussions qui s'élevèrent entre D. Bernoulli, d' Alembert, Lagrange et lui-même le conduisirent à préciser la notion générale de fonction, sous une forme voisine de celle que l'on adopte maintenant : fonctions « arbitraires » données expérimentalement par un ou plusieurs arcs de courbes.
En hydrostatique, il généralise, en 1755, le principe de A. Clairaut et, la même année, il établit les équations générales de l'hydrodynamique.
Ses travaux d'astronomie se rattachent pour la plupart à la mécanique. L'étude des perturbations mutuelles de Jupiter et de Saturne fut proposée comme sujet de prix par l'Académie des sciences de Paris en 1748 et 1752. Il remporta les deux prix. Sur le mouvement parabolique des planètes, il publia, dès 1744, la formule dite de Lambert liant pour deux positions de l'astre, l'intervalle de temps, la corde et les deux rayons vecteurs.
Dans un travail de 1749 sur la précession des équinoxes, partant d'équations plus simples que celles de d'Alembert, il présente les résultats avec plus d'élégance. En 1753, dans sa théorie du mouvement de la Lune, qu'il améliore en 1772, il cherche à établir toutes les inégalités, remportant à ce sujet les prix de l'Académie des sciences de Paris pour 1770 et 1772.
En optique, Euler, à peu près seul parmi ses contemporains, soutenait une théorie ondulatoire de la lumière, comme on peut le voir dans ses Lettres à une princesse d'Allemagne. Pour lui, revenant aux conceptions de C. Huygens, « la lumière n'est autre chose qu'une agitation ou ébranlement causé par les particules de l'éther », « chaque couleur simple étant attachée à un certain nombre de vibrations qui s'achèvent dans un certain temps ».Jean Itard
Autres sciences
Leonhard Euler a également contribué à d'autres sciences, comme certains domaines des sciences physiques, en étudiant par exemple le mouvement de la Lune.
Physique et astronomie
Euler a contribué à l'élaboration de la théorie d'Euler-Bernoulli, qui est un modèle utilisé dans le domaine de la résistance des matériaux. En dehors de l'application avec succès de ses outils d'analyse aux problèmes liés à la mécanique newtonienne, Euler a également appliqué ses techniques à des problèmes d'astronomie. Ses travaux dans cette science ont été reconnus par un certain nombre de prix décernés par l'Académie de Paris au cours de sa carrière. Ses réalisations comprennent la détermination avec une grande précision des orbites des comètes et des autres corps célestes, mais aussi la compréhension de la nature des comètes, et le calcul de la parallaxe du Soleil. Ses calculs ont également contribué à l'élaboration de tables précises de longitudes.
En dynamique des fluides, Euler fut le premier à poser les équations désormais connues sous le nom d'équations d'Euler des fluides parfaits, dans Mémoires de l'Académie royale des sciences et des belles lettres de Berlin 1757. Elles permettent le calcul de nombreux écoulements, comme la circulation sanguine, l'aérodynamique des automobiles et des avions, l'hydraulique, l'océanographie, la météorologie ou la grande tache rouge de Jupiter.
En outre, Euler a fait d'importantes contributions en optique. Il a exprimé son désaccord avec la théorie corpusculaire de la lumière de Newton dans Opticks, qui était alors la théorie dominante. Ses documents des années 1740 sur l'optique ont contribué à faire en sorte que la théorie ondulatoire de la lumière proposée par Christian Huygens devienne la théorie la plus largement répandue, au moins jusqu'au développement de la théorie quantique de la lumière.
Il est aussi crédité pour avoir, avec l'aide des courbes fermées, illustré le raisonnement syllogistique, en 1768. Ces schémas sont désormais connus sous le nom de diagrammes d'Euler. Ainsi, le diagramme de gauche illustre le syllogisme suivant :
Illustration d'un syllogisme de la deuxième figure par un diagramme d'Euler.
Aucun prêtre n'est un singe.
Or, les chimpanzés sont des singes.
Donc, les chimpanzés ne sont pas prêtres.
Philosophie personnelle et croyances religieuses
Leonhard Euler et son ami Daniel Bernoulli ont été des adversaires de la Monadologie de Leibniz et de la philosophie de Christian Wolff. Euler a insisté sur le fait que la connaissance est fondée en partie sur la base de lois quantitatives précises. Les tendances religieuses d'Euler pourraient aussi avoir eu une incidence sur son aversion de la doctrine, il est allé jusqu'à qualifier les idées de Wolff de sauvages et athées.
Beaucoup de ce qui est connu des croyances religieuses d'Euler peut être déduit de ses Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie et d'un ouvrage antérieur, Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister. Ces écrits montrent qu'Euler était un fervent chrétien qui estimait que la Bible avait été inspirée.
Une anecdote rapportée par Dieudonné Thiébault56 met en scène les croyances religieuses d'Euler. Le philosophe français Denis Diderot, en visite à Saint-Pétersbourg en 1773-1774, avait accepté, à la demande de l'impératrice Catherine II, de voir la preuve de l'existence de Dieu qu'Euler prétendait pouvoir produire. Les deux hommes se rencontrèrent donc et Euler, sur un ton d'une parfaite conviction annonça Monsieur, a + bn/n = x ; donc Dieu existe, répondez ! . Le désarroi de Diderot, pour qui, selon l'anecdote les mathématiques étaient incompréhensibles, provoqua les rires de la cour. Gêné, il demanda à quitter la Russie. Il est plus que probable que l'anecdote soit apocryphe et Thiébault ne prétend pas le contraire. De toute évidence, ce dernier n'était pas présent, ses mémoires sont tardifs, la formule soi-disant donnée par Euler n'a aucun sens et Diderot n'était pas étranger aux mathématiques – comme en atteste la réputation qu'il s'était faite avec ses Mémoires sur différents sujets de mathématiques entre autres.
Publications
La couverture de Methodus inveniendi lineas curvas, écrit par Euler
Leonhard Euler a beaucoup écrit. Ses ouvrages les plus connus sont :
Éléments d'algèbre — Cet ouvrage d'algèbre élémentaire commence par une discussion sur la nature des nombres et donne une introduction à l'algèbre, incluant les formules pour les solutions d'équations polynomiales. Écrit en 1765 en allemand sous le titre Vollständige Anleitung zur Algebra, traduction en russe publiée en 1770 par l'Académie des sciences de Saint-Pétersbourg, puis :
1re éd. en allemand en 1770, en 2 volumes ; vol. 1 : E387, vol. 2 : E388 ou 1 ;
traduit en français :
en 1774 par Jean III Bernoulli,
en 1807 par Jean-Guillaume Garnier : vol. 1 et 2 ;
traduit en anglais à partir des versions en français :
en 1797 par Francis Horner 2e éd. : Johnson, 1810, incluant la traduction des Additions de 1774 par Lagrange, aperçu sur Google Livres,
en 1822 par John Hewlett, éd. Longman, aperçu sur Google Livres,
en 1824 par Charles Tayler.
Introductio in analysin infinitorum, Marcum-Michaelem Bousquet & socios, 1748, Livre I :Livre II :
Lettres à une Princesse d'Allemagne, Barthelemy Chirol, Genève, 1775
Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti, 1744 ; le titre latin se traduit par Une méthode pour trouver des lignes courbes jouissant de propriétés de maximum ou de minimum, ou la solution de problèmes isopérimétrique dans le sens le plus large.
Tractatus de numerorum doctrina capita sedecim, quae supersunt E792, 1849 : une introduction à la théorie des nombres, qu'Euler avait commencé à rédiger vers 1750 et annotée plus tard, puis abandonnée.
Une collection définitive des travaux d'Euler, nommée Opera Omnia, a été publiée en 1911 par la Commission Euler de l'Académie suisse des sciences naturelles.
Hommages et distinctions
Euler est représenté sur la sixième série des billets suisses de 10 francs, sur de nombreux timbres postaux suisses, allemands et russes.
L'astéroïde 2002 Euler a été nommé en son honneur.
Euler est également honoré par l'Église luthérienne dans son calendrier des saints, le 24 mai.
   
Posté le : 17/09/2016 19:00
|
|
|
|
|
Jean-Nicolas Corvisart-Desmarets |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Le 18 septembre 1821 meurt Jean-Nicolas Corvisart-Desmarets
à Paris, né à Dricourt Ardennes le 15 février 1755, médecin clinicien et professeur français. Il est surtout connu pour avoir été le médecin personnel de l'Empereur français Napoléon Ier. Il travaille au collège de France de 1796 à 1804, il est fait officier de la légion d'honneur puis commandeur de l'order de la Réunion membre de l'académie de médecine
En bref
Clinicien français éminent, Corvisart a soutenu sa thèse de docteur en médecine, en 1782, sur L'Agrément de l'étude de la médecine et les désagréments de sa pratique. Médecin de l'hôpital de la Charité 1788, il obtient, en 1797, la chaire de clinique interne à la Faculté de médecine, puis celle de médecine au Collège de France. Sa réputation d'excellent clinicien le fait nommer auprès de Bonaparte, dont il dissipe les malaises par une hygiène alimentaire stricte. Il suit le destin de son client : premier médecin de Leurs Majestés Impériales 1804, il participe à quelques campagnes Italie 1805, Autriche 1809 ; il soigne Joséphine évanouie à l'annonce de son divorce, et aide Dubois, affolé, à accoucher Marie-Louise, qu'il suivra dans son premier exil à Blois. Atteint d'hémiplégie en 1816, il craint que la maladie ne lui fasse commettre des erreurs de diagnostic, cesse de soigner et d'enseigner et passe ses dernières années à observer l'évolution de son mal.
Il ne doit cependant pas sa célébrité à l'Empereur, mais à son exceptionnel sens clinique et à ses dons d'enseignant à la Charité. Son Essai sur les maladies du cœur et des gros vaisseaux 1806 établit la pathologie cardiovasculaire ; il introduit, perfectionne et enseigne la technique de la percussion d'Auenbrugger (dont il traduit l'ouvrage sous le titre Nouvelle Méthode pour reconnaître les maladies internes de la poitrine, 1808) et l'applique au diagnostic des maladies cardiaques. En outre, il a créé l'enseignement anatomoclinique au lit du malade, tel qu'il est pratiqué depuis lors : étude des cas, visite du malade et discussion avec les élèves, vérification anatomique, surveillance de l'évolution, cours magistraux appuyés sur les cas observés. « Je ne crois pas à la médecine, je crois en Corvisart », disait Napoléon qui le fit baron d'Empire. Jacqueline Brossolet
Sa vie
Fils d'un procureur au parlement de Paris, il naît pendant l'exil du parlement et fait ses humanités au collège Sainte-Barbe. Malgré les désirs de son père, qui le destinait au barreau, et après une rencontre décisive avec Antoine Petit, « le seul médecin de Paris qui sache opérer et accoucher », le jeune Jean-Nicolas entame des études médicales auprès des professeurs de l'Hôtel-Dieu, où il devient aide-soignant lorsque son père lui coupe les vivres.
Il étudie ainsi auprès de Pierre-Joseph Desault, Félix Vicq d'Azyr, Antoine Petit, Louis Desbois de Rochefort, Philippe Pelletan. Le 14 novembre 1782, il reçoit le titre de docteur-régent de la faculté, mais comme il se refuse de porter la perruque, on lui interdit d'entrer comme médecin à l'hôpital des Paroisses et il doit accepter un poste dans un hôpital pour pauvres du quartier de Saint-Sulpice.
À l'hôpital de la Charité, il est suppléant de Desbois de Rochefort, qu'il remplace en 1788. Il y introduit des réformes profondes qu'il dirige d'une main de fer. Il y est bientôt nommé professeur de pathologie, puis de physiologie. René Laennec et Jean-Etienne Esquirol font partie de ses nombreux élèves.
L'enseignement de la médecine est supprimé par la Révolution en 1792 et les charlatans pullulent, mais dès la fin de 1794 on recommence à réglementer les études. Corvisart continue les leçons de Desbois d'une manière si brillante que, lors de la création de l'École de médecine, instituée par décret du 14 frimaire an III, il y obtient la chaire de clinique interne. L'école de Paris devient bientôt l'une des plus réputées d'Europe. Deux ans plus tard, il est professeur de médecine pratique au Collège de France, où il est titulaire de la chaire de médecine en 1797.
À l'hôpital de la Charité, il réorganise son service en donnant la priorité à la percussion du malade au lit et à l'anatomie pathologique. Il y fait également construire un amphithéâtre d'anatomie. Il s'intéresse surtout à la cardiologie, rendant le diagnostic plus précis, par exemple grâce à la percussion de la paroi thoracique. Il insiste dans son enseignement sur la nécessité de pratiquer dès le début un examen attentif et systématique.
Dans les premières années du xixe siècle, il gagne la confiance de Napoléon Bonaparte et de Joséphine de Beauharnais, dont il devient en 1804 le médecin personnel. En l'an X, le premier Consul l'attache à son service personnel. Napoléon est fasciné par son calme et la sûreté de son diagnostic et il aurait dit : « Je ne crois pas à la médecine, mais je crois en Corvisart. » Il le nomme chevalier deux ans seulement après la création de la Légion d'honneur, en 1804. Corvisart accompagne Napoléon en Italie en 1805 et en Autriche en 1809. Il soigne aussi Joséphine qui exige de plus en plus de pilules, et à qui il prescrit des placebos.
Sa réponse à Napoléon est restée célèbre. L’empereur, qui pensait à se séparer de Joséphine, lui avait demandé : « Un homme de soixante ans qui épouse une jeune femme a-t-il encore des enfants ? – Quelquefois. – Et à soixante et dix ? – Toujours, Sire.
Membre et officier de la Légion d'Honneur les 26 frimaire et 25 prairial an XII, il devient baron de l'Empire à l'institution de la nouvelle noblesse en 1808. Déjà commandeur de l'Ordre de l'Union, il fait partie de la première nomination des commandeurs de l'ordre de la Réunion, le 29 février 1812.
Élu membre de l'Académie des sciences en 1811 et de l'Académie de médecine en 1820, il appartient à presque toutes les sociétés savantes de l'Europe.
L'un de ses ouvrages majeurs est son Essai sur les maladies et les lésions organiques du cœur et des gros vaisseaux, paru en 1806. En 1808, il traduit le livre de Leopold Auenbrugger sur la percussion.
Il est le propriétaire de Château des Tournelles à La Garenne-Colombes de 1806 au 24 avril 1820.
Il meurt en 1821 à Paris après plusieurs attaques cérébrales, quelques mois seulement après la mort de Napoléon à Sainte-Hélène. Napoléon avait dit de lui : C'est un honnête et habile homme.
Il est enterré au cimetière d'Athis Mons. Deux de ses descendants reposent dans le même caveau : Lucien, baron Corvisart, médecin de Napoléon III ; Scipion, général, qui prit part à la bataille de Verdun en 1917. La tombe de Nicolas Corvisart provient de l'ancienne ferme du château d'Athis dont il était devenu propriétaire en 1812 ; son neveu et héritier vendant l'exploitation, ses restes ont été exhumés et transférés dans le cimetière de la commune en 1824.
Une rue depuis 1867, un lycée, une station de métro de Paris et un complexe hospitalier à Charleville-Mézières, fermé depuis 2011, portent son nom.
Œuvres et publications
Essai sur les maladies et les lésions organiques du cœur et des gros vaisseaux, extrait des leçons cliniques, imp. de Migneret (Paris), 1806, Texte intégral
Essai sur les maladies et les lésions organiques du cœur et des gros vaisseaux, imp. de Mame, 1811, Lire en ligne
Essai sur les maladies et les lésions organiques du cœur et des gros vaisseaux suivi de Nouvelle méthode pour reconnaitre les maladies internes de la poitrinepar Avenbrugger, suivi de Recherches sur la phthisie pulmonaire par Bayle ,A. Delahays Paris, 1855, Texte intégral , disponible sur Gallica
Armoiries
Blasonnement
Armes de baron de l'Empire :
Ecartelé : au I, d'or au cœur de gueules ; au II, du quartier des Barons tirés des Corps Savants ; au III, de gueules au lion d'argent ; au, IV d'argent au serpent de sinople enlaçant une cotice alesée de sable bâton d'Esculape en pal.
   
Posté le : 17/09/2016 16:55
|
|
|
|
|
Saint exupéry |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Le 31 juillet 1944 meurt Antoine de Saint-Exupéry
à 33 ans, disparu en vol, en mer au large de Marseille, alias Saint Ex, mort pour la France, écrivain, poète, aviateur et reporter français, né le 29 juin 1900 à Lyon.
Il reçoit pour distinction le prix Femina, le Grand prix du roman de l'Académie française pour ses romans, récits, contes, et essais. Ses Œuvres principales sont Courrier sud en 1929, Vol de nuit en 1931, Terre des hommes en 1939, Lettre à un otage en 1940, Pilote de guerre en 1942, Le Petit Prince en 1943.
En bref
Né dans une famille issue de la noblesse française, Antoine de Saint-Exupéry passe une enfance heureuse malgré la mort prématurée de son père. Élève peu brillant, il obtient cependant son baccalauréat en 1917 et, après son échec à l'École navale, il s'oriente vers les beaux-arts et l'architecture. Devenu pilote lors de son service militaire en 1921 à Strasbourg, il est engagé en 1926 par la compagnie Latécoère future Aéropostale et transporte le courrier de Toulouse au Sénégal avant de rejoindre l'Amérique du Sud en 1929. Parallèlement il publie, en s'inspirant de ses expériences d'aviateur, ses premiers romans : Courrier sud en 1929 et surtout Vol de nuit en 1931, qui rencontre un grand succès.
À partir de 1932, son employeur entre dans une période difficile. Aussi Saint-Exupéry se consacre-t-il à l’écriture et au journalisme. Il entreprend de grands reportages au Viêt Nam en 1934, à Moscou en 1935, en Espagne en 1936, qui nourriront sa réflexion sur les valeurs humanistes qu'il développe dans Terre des hommes, publié en 1939.
En 1939, il sert dans l'armée de l'air où il est affecté dans une escadrille de reconnaissance aérienne. À l'armistice, il quitte la France pour New York avec pour objectif de faire entrer les Américains dans la guerre et devient l'une des voix de la Résistance. Rêvant d'action, il rejoint enfin, au printemps 1944, en Sardaigne puis en Corse, une unité chargée de reconnaissances photographiques en vue du débarquement de Provence. Il disparaît en mer avec son avion un Lockheed P-38 Lightning lors de sa mission du 31 juillet 1944. Son avion n'a été retrouvé qu'à partir de 2000 au large de Marseille.
Le Petit Prince, écrit à New York pendant la guerre, est publié avec ses propres aquarelles en 1943 à New York et en 1946 chez Gallimard, en France. Ce conte plein de charme et d'humanité devient très vite un immense succès mondial.
« Pour moi, voler ou écrire, c'est tout un. Les lauriers que l'épopée aérienne valut à l'aviateur-poète Antoine de Saint-Exupéry ont cessé d'auréoler son œuvre. La question est de savoir si le poète-aviateur a su conférer à l'éphémère d'une actualité, même prestigieuse, valeur d'éternité. Le mythe envolé, que reste-t-il ? Restent ce que Roger Caillois a nommé des rapports, mais rapports d'une prise de conscience progressive de soi et des autres, d'une connaissance créatrice dont les moyens furent autant la solitude et la guerre que l'avion, merveilleux instrument d'analyse, thème d'inspiration et tremplin des relations humaines. De L'Aviateur – qui se réfère à un métier – à Citadelle – qui évoque un monument – s'élabore dans le courage, l'obstination et la générosité une « expérience morale » à laquelle ont œuvré conjointement l'aventure et l'écriture, sans que la seconde pipe la première ou s'y substitue ; c'est pourquoi Caillois a pu conclure : « À une époque où la littérature sert communément d'alibi, cette honnêteté luxueuse apporte tout ensemble une preuve de la grandeur de l'indépendance d'un écrivain et d'une œuvre » préface à l'édition de La Pléiade.
Sa vie
Fils du vicomte Martin Louis Marie Jean de Saint Exupéry 1863-1904, 37 ans et sans profession, et de Andrée Marie Louise Boyer de Fonscolombe, 25 ans, Antoine Jean-Baptiste Marie Roger de Saint Exupéry naît le 29 juin 1900 au 8, rue du Peyrat, dans le 2e arrondissement de Lyon dans une famille issue de la noblesse française. Il partage une enfance heureuse avec ses quatre frères et sœurs. Mais en 1904, son père meurt, terrassé par une hémorragie cérébrale à seulement 41 ans, en gare de Foux, laissant Marie de Saint-Exupéry éduquer seule ses cinq enfants : Marie-Madeleine, dite Biche, Simone, dite Monot, Antoine, dit Tonio, François et Gabrielle, dite Didi.
La mère d'Antoine vit mal ce veuvage prématuré, mais son naturel optimiste lui permet de faire face à ses obligations. D'une sensibilité à fleur de peau, artiste elle fait de la peinture, elle tisse avec Antoine des liens privilégiés et lui offre une excellente éducation, chose difficile à l'époque pour une femme seule. Elle transmet à son fils adoré des valeurs qu'il conservera toute sa vie : honnêteté, respect d'autrui, pas d'exclusivité sociale. Femme exceptionnelle, elle consacre sa vie à ses enfants, avec un humanisme que Saint-Exupéry a cultivé tout au long de ses voyages.
Jusqu'à dix ans, il passe son enfance entre le château de La Môle dans le Var, propriété de sa grand-mère maternelle, et le château de Saint-Maurice-de-Rémens dans l'Ain, propriété de sa tante Madame Tricaud. À la fin de l'été 1909, sa famille s'installe au Mans, région d'origine de son père. Antoine entre au collège Notre-Dame de Sainte-Croix le 7 octobre suivant. Attiré par l'ailleurs, le lointain, l'aventure, il cherche depuis l'enfance à échapper aux bornes de son milieu aristocratique.
En 1912, iasse les grandes vacances à Saint-Maurice-de-Rémens. Fasciné par les avions, il se rend souvent à vélo à l’aérodrome d'Ambérieu-en-Bugey, situé à quelques kilomètres et y reste des heures à interroger les mécaniciens sur le fonctionnement des avions. Un jour, il s'adresse au pilote Gabriel Salvez en prétendant que sa mère l'a autorisé à effectuer un baptême de l'air. Il fait donc son baptême sur un Berthaud Wroblewski, avion fabriqué à Villeurbanne par l'industriel lyonnais Berthaud sur des plans de Pierre et Gabriel Wroblewski-Salvez. Il écrit un poème témoignant de sa nouvelle passion pour les avions :
Les ailes frémissaient sous le souffle du soir
Le moteur de son chant berçait l'âme endormie
Le soleil nous frôlait de sa couleur pâle.
Saint-Exupéry passe ainsi presque toute son enfance dans le château familial, entouré de ses frères et sœurs. Il se souviendra de cette période comme celle du paradis perdu : « Les plus beaux moments de ma vie, dira-t-il plus tard. En revanche, il ne se plaît pas beaucoup au collège Sainte-Croix du Mans où il est pensionnaire. Ses camarades, qui le surnomment Tatane, collaborent toutefois au journal de classe créé à son initiative, qui sera ensuite interdit par les Pères.
Alors que la Première Guerre mondiale éclate, Marie de Saint-Exupéry est nommée infirmière-chef de l'hôpital militaire d'Ambérieu-en-Bugey dans l'Ain. Grâce à son travail, elle peut faire venir ses enfants près d'elle. Ses deux fils, Antoine et François, intègrent en tant qu'internes le collège jésuite de Notre-Dame de Mongré, à Villefranche-sur-Saône. Le jeune Antoine peut donc enfin se consacrer à l'écriture, avec brio, puisque, même si ses études sont médiocres par ailleurs, il remporte le prix de narration du lycée pour l'une de ses rédactions.
À la rentrée scolaire de 1915, Marie de Saint-Exupéry, toujours en poste à Ambérieu-en-Bugey, estime que ses fils ne se plaisent pas vraiment chez les pères jésuites de Mongré. Soucieuse de protéger ses enfants et de leur donner une éducation qui leur permette de développer leurs dons, elle préfère les inscrire chez les frères marianistes de la Villa Saint-Jean à Fribourg, en Suisse. En rapport étroit avec le collège Stanislas de Paris, ce collège a développé une méthode d'éducation moderne qui leur permet d'exprimer leur créativité. Antoine y retrouve Louis de Bonnevie, dont la famille est voisine et amie de la sienne à Lyon. Il noue avec lui ainsi qu’avec Marc Sabran et Charles Sallès une amitié profonde et durable.
En 1917, il obtient son baccalauréat malgré des résultats scolaires peu brillants. L'élève Saint-Exupéry est davantage à l'aise dans les matières scientifiques que littéraires. Au cours de l'été, souffrant de rhumatismes articulaires, François, le frère cadet d'Antoine, le compagnon de jeux et le confident, meurt d'une péricardite. Attristé par la mort de son frère, Saint-Exupéry vivra cet évènement comme le passage de sa vie d'adolescent à celle d'adulte.
La guerre aussi l'inspire. Il réalise des caricatures de soldats prussiens et de leurs casques à pointe, de l'empereur et du Kronprinz. Il écrit aussi quelques poèmes :
Parfois confusément sous un rayon lunaire,
Un soldat se détache incliné sur l'eau claire ;
Il rêve à son amour, il rêve à ses vingt ans !
Printemps de guerre
En 1919, Antoine échoue au concours de l'École navale ses résultats dans les branches scientifiques sont très bons, mais ceux des branches littéraires insuffisants et s'inscrit en tant qu'auditeur libre en architecture à l'École nationale supérieure des beaux-arts. À la mort de la tante Tricaud, en 1920, Marie hérite du château de Saint-Maurice où elle s’installe. Ses revenus sont modestes, elle subvient aux besoins de ses enfants en vendant les terres attenantes au château. Antoine bénéficie alors de l'hospitalité de sa cousine Yvonne de Lestrange et accepte également plusieurs petits emplois : avec son ami Henry de Ségogne, il sera notamment figurant durant plusieurs semaines dans Quo Vadis, un opéra de Jean Noguès. En 1918, il avait fait la connaissance de Louise de Vilmorin, qui lui inspire des poèmes romantiques.
Je me souviens de toi comme d'un foyer clair
Près de qui j'ai vécu des heures, sans rien dire
Pareil aux vieux chasseurs fatigués du grand air
Qui tisonnent tandis que leur chien blanc respire.
À mon amie
Cependant, durant cette période, son intense activité poétique lui inspire des poèmes plutôt mélancoliques, des sonnets et des suites de quatrains Veillée, 1921 montrant qu'il vit une période difficile, car il se retrouve sans projet de vie et sans perspective d'avenir. Certains de ses poèmes sont calligraphiés et enluminés de dessins à l'encre de Chine. Il offre deux de ses cahiers de poésie à son ami Jean Doat.
Dans l’aviation
En avril 1921, il est affecté pour son service militaire en tant que mécanicien au 2e régiment d’aviation de Strasbourg. En juin, il prend des cours de pilotage à ses frais8. Le 9 juillet son moniteur le lâche pour un tour de piste. Seul aux commandes de son avion-école, il se présente trop haut pour l'atterrissage. Remettant les gaz trop brusquement, il cause un retour au carburateur. Croyant que le moteur a pris feu il ne s'affole pas, fait un second tour de piste et atterrit en beauté. Son moniteur valide sa formation. Néanmoins, il laisse le souvenir d’un aviateur parfois distrait, oubliant tantôt de rentrer son train d’atterrissage, tantôt de brancher ses instruments de bord, se perdant dans l’immensité du ciel. Le surnom de Pique la Lune lui est ainsi resté, non seulement en raison de son nez en trompette mais aussi d’une tendance certaine à se replier dans son monde intérieur.
En janvier 1922, il est à Istres comme élève officier de réserve. Il est reçu pilote militaire et promu caporal. En avril 1922, dans le cadre de sa formation comme EOR, il suit des cours d’entraînement à Avord, qu'il quitte pour la région parisienne avec le grade de sous-lieutenant. Début août, il est affecté au 37e régiment d’aviation à Casablanca, où il obtient son brevet civil. Pendant ses loisirs, il réalise des croquis de ses copains de chambrée au crayon mine de charbon et à l’encre turquoise. Ses dessins sont regroupés dans son cahier Les Copains. En octobre, sous-lieutenant de réserve, il choisit son affectation au 34e régiment d’aviation, au Bourget. Au printemps 1923, il a son premier accident d’avion au Bourget : fracture du crâne. Après ce grave accident, il est démobilisé. Pourtant, il envisage toujours d’entrer dans l'armée de l’air, comme l’y encourage le général Barès. Mais la famille de Louise de Vilmorin, sa fiancée, s’y oppose. Commence pour lui une longue période d’ennui : il se retrouve dans un bureau comme contrôleur de fabrication au Comptoir de Tuilerie, une filiale de la Société générale d’Entreprise. En septembre, c’est la rupture des fiançailles avec Louise.
En 1924, Saint-Exupéry travaille dans l’Allier et la Creuse comme représentant de l’usine Saurer qui fabrique des camions (il n’en vendra qu’un seul en une année et demie !). Il se lasse et donne sa démission. En 1924, il commence aussi une œuvre en prose, Manon, danseuse. En 1925, son poème intitulé La Lune montre une inspiration farfelue. On peut aussi citer la suite poétique L'Adieu :
Il est minuit — je me promène
Et j’hésite scandalisé
Quel est ce pâle chimpanzé
Qui danse dans cette fontaine ?
La Lune, 1925
En 1926, il est engagé par Didier Daurat, directeur de l’exploitation des lignes de la compagnie Latécoère future Aéropostale et rejoint l'aéroport de Toulouse - Montaudran pour effectuer du transport de courrier sur des vols entre Toulouse et Dakar. Il rédige alors une nouvelle L'évasion de Jacques Bernis, dont sera tiré L'Aviateur, publié dans la revue d’Adrienne Monnier, Le Navire d’argent numéro d'avril, où travaille son ami Jean Prévost. À Toulouse, il fait la connaissance de Jean Mermoz et de Henri Guillaumet. Au bout de deux mois, il est chargé de son premier convoyage de courrier sur Alicante.
Consuelo de Saint-Exupery
Fin 1927, il est nommé chef d’escale à Cap Juby au Maroc avec pour mission d’améliorer les relations de la compagnie avec les dissidents maures d’une part et avec les Espagnols d’autre part. Il va y découvrir la brûlante solitude et la magie du désert. En 1929, il publie chez Gallimard son premier roman, Courrier sud, dans lequel il raconte sa vie et ses émotions de pilote.
En septembre 1929, il rejoint Mermoz et Guillaumet en Amérique du Sud pour contribuer au développement de l’Aéropostale jusqu’en Patagonie. En 1930, il utilise la bibliothèque de son ami Paul Dony pour commettre divers sonnets inspirés d’autres poètes mais qui sont autant d’exercices de virtuosité poétique. En 1931, il publie son second roman, Vol de nuit, un immense succès, dans lequel il évoque ses années en Argentine et le développement des lignes vers la Patagonie. Le 22 avril 1931, il se marie à Nice avec Consuelo Suncin Sandoval de Gómez décédée en 1979, à la fois écrivaine et artiste salvadorienne.
À partir de 1932, alors que la compagnie, minée par la politique, ne survit pas à son intégration dans Air France, il subsiste difficilement, se consacrant à l’écriture et au journalisme. Saint-Exupéry demeure pilote d’essai et pilote de raid en même temps qu’il devient journaliste d’occasion pour de grands reportages
Reporter pour Paris-Soir, il voyage au Viêt Nam en 1934 et à Moscou en 1935. Le 29 décembre 1935, accompagné de son mécanicien André Prévot, il tente un raid Paris-Saïgon à bord d'un Caudron-Renault Simoun, pour battre le record d'André Japy qui quelques jours plus tôt a relié Paris à Saïgon en 3 jours et 15 heures. Vers 3 heures du matin le 30 décembre, l'avion heurte un plateau rocheux alors que Saint-Exupéry avait volontairement diminué son altitude pour tenter de se repérer. Les deux aviateurs sont indemnes mais perdus dans le désert Libyque, en Égypte. Ils connaissent alors trois jours d'errance sans eau ni vivres avant un sauvetage inespéré.
En 1936, Saint-Exupéry est envoyé comme reporter en Espagne pour couvrir la guerre civile. Parce qu'il refuse d'adopter une conception bassement partisane du journalisme, à l'inverse de tous les intellectuels de son temps, il décide de révéler les exactions des républicains espagnols. De tous ces voyages, il accumule une très importante somme de souvenirs, d’émotions et d’expériences, qui lui servent à nourrir sa réflexion sur le sens à donner à la condition humaine. Sa réflexion aboutit à l’écriture de Terre des hommes, qui est publié en 1939. L’ouvrage est récompensé par le prix de l’Académie française. C’est dans ce roman que l’on trouve la célèbre phrase prononcée par Henri Guillaumet après son accident dans les Andes : Ce que j’ai fait, je te le jure, jamais aucune bête ne l’aurait fait.
Guerre de 1939-1945
En 1939, il sert comme capitaine dans l'Armée de l'air où il est affecté dans une escadrille de reconnaissance aérienne. Le 23 mai 1940, il survole Arras alors que les panzers allemands envahissent la ville : bien que son avion Bloch 174 soit criblé de balles par la DCA allemande, il réussit à retourner à la base de Nangis avec ses passagers sains et saufs, ce qui lui vaut d'être récompensé de la Croix de guerre avec palme et cité à l’ordre de l’Armée de l’air, le 2 juin 1940. Cet exploit lui inspirera le titre et la trame de Pilote de guerre. À l'armistice, il quitte la France pour New York avec pour objectif de faire entrer en guerre les Américains. Considéré par certains comme pétainiste car non gaulliste, Saint-Exupéry a du mal à faire entendre sa voix. Comme l’immense majorité des Français, il est au départ plutôt favorable à Vichy, qui lui semble représenter la continuité de l'État, et qui représente une cohésion nationale pour les Français souffrant de l'Occupation, et donc plutôt méfiant envers le général de Gaulle. De fait, il a surtout essayé de réconcilier les factions opposées ; lors de son appel radiophonique du 29 novembre 1942 depuis New York, soit trois semaines après le débarquement allié en Afrique du Nord, il lance : Français, réconcilions-nous pour servir; Il tente aussi de repousser l'épuration qui se prépare, mais il est incompris, il est trop tard et le temps est celui de l'affrontement général. Cependant, selon des archives américaines récemment ouvertes, il semblerait que les services secrets américains aient envisagé de le pousser en lieu et place du général de Gaulle.
En mai 1942, il séjourne au Canada dans la famille De Koninck, rue Sainte-Geneviève, dans le vieux-Québec. Alors que son séjour devait durer quelques jours, il passe finalement près de cinq semaines au Québec à cause de problèmes de visa. Gardant pour mission de faire entrer les Américains dans la guerre, il publie à New York en février 1942 Pilote de guerre pour rappeler aux Américains combien la bataille de France avait été dure, avant de publier un an plus tard le conte poétique et philosophique Le Petit Prince.
Mais il ne pense qu'à s'engager dans l'action, considérant, comme ce fut le cas avec l'Aéropostale, que seuls ceux qui participent aux événements sont légitimes pour en témoigner. En avril 1943, bien que considéré par les Alliés comme un pilote dépassé, incapable de piloter un avion de combat moderne, il reprend du service actif dans l'aviation en Tunisie grâce à ses relations et aux pressions du commandement français. Toujours dans la reconnaissance aérienne, il effectue quelques missions, mais il est victime de plusieurs incidents qui le font mettre en réserve de commandement, étant donné son âge, son mauvais état de santé général, ses différents crashs précédents. Il séjourne alors en Algérie, au Maroc, puis en Algérie de nouveau, où il obtient au printemps 1944 l'autorisation du commandant en chef des forces aériennes en Méditerranée, le général américain Eaker, de rejoindre le prestigieux groupe 2/33 basé à Alghero, en Sardaigne, avec le grade de commandant. Il effectue plusieurs vols, émaillés de pannes et d'incidents. Le 17 juillet 1944, le 2/33 s'installe à Borgo, non loin de Bastia, en Corse. C'est de l'aéroport voisin de Poretta qu'il décolle aux commandes de son F-5B-1-LO, version photo du bimoteur P-38 Lightning, le 31 juillet à 8 h 25 du matin, pour une mission de cartographie cap sur la vallée du Rhône, cap sur Annecy et retour par la Provence : des reconnaissances photographiques afin de tracer des cartes précises du pays, fort utiles au tout prochain débarquement en Provence, prévu pour le 15 août. Il est seul à bord, son avion n'est pas armé et emporte du carburant pour six heures de vol. À 8 h 30, est signalé le dernier écho radar. Son avion se serait écrasé à quelques encablures des côtes de la Provence. Il est alors impossible d'effectuer des recherches sur le terrain en temps de guerre. Saint-Ex est officiellement porté disparu. Sa mémoire est célébrée solennellement à Strasbourg le 31 juillet 1945. En 1948, il est reconnu Mort pour la France. Après la disparition de son fils, Marie se réfugie dans la prière, écrit des poèmes où elle parle de son fils et fait publier ses écrits posthumes.
La double vocation
Lorsque, au soir de son baptême de l'air, Antoine de Saint-Exupéry, alors âgé de douze ans, offrit à son professeur de français un poème aéronautique, peut-être pressentait-il la double orientation qu'allait prendre son destin. Cependant, les chemins qui l'y menèrent furent moins directs qu'on le pourrait supposer.
De père limousin, provençal par sa mère, aristocrate des deux côtés, il naquit à Lyon, le troisième de six enfants. Orphelin de père dès ses quatre ans, il reçut une formation classique dans des instituts religieux. Tôt il manifesta une propension pour la mécanique où l'imagination a sa part. Élève irrégulier, paraît-il, tempérament indiscipliné, il fut néanmoins bachelier à dix-sept ans. Après avoir échoué au concours d'entrée à l'École navale, il tenta l'architecture pour retrouver volontairement l'avion lors de son service militaire (1921-1923).
Il y commet son premier exploit en s'emparant d'un appareil pour effectuer un vol solitaire qui faillit se terminer en catastrophe, mais révéla le sang-froid du pilote et cette maîtrise qui va chez lui de pair avec une sorte de témérité et presque un goût de l'aventure marginale. L'armée de l'air s'ouvre à lui ; il y renonce devant l'opposition de la famille de sa fiancée. Mais ni la bureaucratie ni la vente de camions pour les usines Saurer ne le consolent de l'avion qu'il rejoint chaque fois qu'il le peut. 1926 fut une année décisive : engagé à la société d'aviation Latécoère, il débute en octobre à Toulouse, sous la direction de Didier Daurat, le futur Rivière de Vol de nuit, le type même du chef, à la fois maître et entraîneur. Au début de la même année, il avait publié une nouvelle, L'Aviateur ; dorénavant, les écrits marqueront les jalons moins d'une carrière que d'une aventure, dont ils feront le point et dont ils seront le prolongement éthique et poétique.
Envoyé en 1927 comme chef de base à Cap Juby (Río de Oro), escale aussi dangereuse que vitale sur la ligne Casablanca-Dakar, Saint-Exupéry découvre à la fois l'action responsable, le désert et les Maures. Maintes fois, il sauva des aviateurs en panne ou captifs des dissidents. Le soir, il écrit Courrier Sud (1928). Dans ce récit, influencé sur le plan romanesque par la manière de Gide, le narrateur rapporte les confidences d'un pilote de l'Aéropostale qui, peu avant de s'écraser sur les sables, a connu la mort d'un amour. « Le roman d'un aviateur l'emporte sur le roman de l'aviation » (Luc Estang), non sans en amorcer les composantes essentielles : le sens de la fraternité virile, et surtout cette optique fondamentale de Saint-Exupéry pour qui l'avion fut l'outil privilégié qui mêle « l'homme à tous les vieux problèmes ».
Simple comme une épure, mais de chair et de sang, Vol de nuit (1931), dans sa sobriété toute classique, est peut-être l'œuvre la plus accomplie de Saint-Exupéry. Son héros, Rivière, autant qu'à Daurat se réfère à l'auteur, directeur depuis octobre 1929 de l'Aeroposta Argentina. Saint-Exupéry a donc éprouvé personnellement les résonances humaines du métier, des responsabilités et de l'exigence du chef à l'héroïque camaraderie de l'équipe, ainsi que cette part d'absolu enclose dans l'immédiat des décisions et des actes. Tel apparaît, lors de la mort de Fabien, le constat de Rivière devant le bonheur détruit de l'épouse : « Si la vie humaine n'a pas de prix, nous agissons toujours comme si quelque chose dépassait, en valeur, la vie humaine... Mais quoi ? »
1931, c'est le mariage avec Consuelo Suncin, le succès du prix Fémina, mais aussi les déboires de l'Aéropostale, le départ de Daurat et le début d'ennuis financiers. De son entrée à Air France en 1934 jusqu'à la veille de la guerre, Saint-Exupéry déploie une activité intense qui le promène d'un bout du monde à l'autre, d'inventions en expérimentations et d'exploits en accidents dont, en 1937, le cinquième depuis le début de sa carrière le force à une immobilité propice au travail littéraire.
Terre des hommes (1939) lui vaut le grand prix du roman de l'Académie française, sans doute parce que la « philosophie » et la poétique de l'aviation qui dominent cet essai sont imbriquées dans la texture même des événements. Qu'il s'agisse, en effet, du sauvetage de Guillaumet dans la cordillère des Andes, des cinq jours d'angoisse et d'errance à travers le désert après la chute survenue au cours du raid Paris-Saigon, d'un reportage sur le front de la guerre d'Espagne ou de menus faits comme le parcours en bus avec les travailleurs matinaux et la rencontre avec le jeune émigré polonais (Mozart assassiné), c'est toujours de la matière vivante, fondue au creuset de l'esprit et du cœur, qu'émergent les repères d'un humanisme. Et quand la guerre met tout en question, Saint-Exupéry commence par s'engager en rejoignant, malgré ses handicaps physiques, un groupe de reconnaissance. Puis, lucidement, dans Pilote de guerre (1942), rédigé à New York, il affirme, par-delà l'absurdité de la guerre et la détresse de la défaite, la nécessité du combat pour la défense du respect et des droits de l'homme. Lettre à un otage 1943 reprend ce thème.
En novembre 1942, un appel à l'union des Français lancé à la radio des États-Unis lui aliène nombre de compatriotes. Il brûle de reprendre le combat et, malgré son âge, obtient l'autorisation de missions. Son unité est basée à Alghero Sardaigne, puis à Borgo Corse. Le 31 juillet 1944, Saint-Exupéry décolle pour une mission de reconnaissance sur la vallée du Rhône. Il n'en reviendra pas. En 2000, des morceaux de son appareil seront retrouvés en Méditerranée, au large de Marseille.
La citadelle sur le sable
Centrée sur les expériences d'un homme, l'œuvre de Saint-Exupéry n'en gardait que ce qui intéressait tous les hommes. À travers romans ou fables Le Petit Prince, 1943 s'édifiait un humanisme. Dès 1936, l'auteur travaillait à une synthèse, de forme allégorique. Au lieu de la somme rêvée, Citadelle 1948 n'est qu'un livre inachevé, mélange de pages d'anthologie et d'ébauches, un ensemble de notes et d'improvisations que, selon ses habitudes de composition, il eût peut-être fondues en une parabole riche de la quintessence de son message.
Si l'ouvrage tel qu'il se présente trahit évidemment la visée initiale, il permet cependant de nuancer l'éthique un peu lapidaire des textes antérieurs et, de même que les Carnets 1953, contribue à démythifier le héros. Car les fragments qu'on possède, écrits en majorité pendant la guerre, témoignent de plus de tâtonnements que de stabilité, et les contradictions, d'ailleurs conscientes, s'y affirment. Avec non moins d'objectivité que de finesse, Luc Estang a exploré ce bazar d'idées. Et, parmi les thèmes familiers qui firent la célébrité de l'auteur – la ferveur constructive, une morale virile fondée sur le service et le dépassement, les relations humaines conçues comme l'essence de l'être –, le critique constate les faiblesses d'une optique sociale plutôt paternaliste, les limites d'une civilisation foncièrement aristocratique dont le seigneur peut aisément devenir le tyran. Il suggère que « l'humanisme de Saint-Exupéry oscille constamment entre l'Évangile du Christ et le contre-Évangile de Nietzsche, comme s'il tentait de reconvertir à leur source religieuse des valeurs subversives dont la virulence s'y infiltrerait. Son réalisme spiritualiste penche vers un spiritualisme relativiste dont le Dieu nécessaire apparaît peu consistant.
Si la «mouvance des sables n'infléchit pas la démarche de Saint-Exupéry, elle l'accule à remettre tout en question, jusqu'au sens du langage. Citadelle ne signifie donc pas installation ni dogmatisme ; elle serait plutôt le symbole de la fermeté de l'esprit et de la fidélité à l'homme, quoi qu'il arrive.
Poète de l'avion au même titre que le marin Joseph Conrad fut « le romancier de la mer », Antoine de Saint-Exupéry, sans en posséder ni la dimension ni les registres, fait penser à Malraux dont il a sans cesse vécu l'engagement autant que la quête de l'absolu. Hubert Hardt
Le mystère de sa mort
Le 12 mars 1950, au Journal officiel, le commandant Antoine de Saint-Exupéry est cité à l'ordre de l'armée aérienne à titre posthume, pour avoir prouvé, en 1940 comme en 1943, sa passion de servir et sa foi en le destin de la patrie, et trouvé une mort glorieuse, le 31 juillet 1944, au retour d'une mission de reconnaissance lointaine sur son pays occupé par l'ennemi .
Si la mort ne fait désormais plus de doute, reste à en élucider les circonstances. En 1950, un pasteur d'Aix-la-Chapelle, ancien officier de renseignements dans la Luftwaffe, témoigne avoir appris, le 31 juillet 1944, qu'un P-38 Lightning avait été abattu en Méditerranée par un Focke-Wulf allemand. Puis, en 1972, surgit dans une revue allemande à caractère historico-fictionnel le témoignage "posthume" d'un jeune officier allemand, l'aspirant Robert Heichele, qui aurait fait feu sur le Lightning depuis son appareil, un Focke-Wulf 190, vers midi, au-dessus de Castellane dans le département des Alpes-de-Haute-Provence. Mais Heichele fut à son tour abattu en août 1944, échappa à la mort, mais fut très grièvement blessé en ayant essayé d’atterrir à Avignon son avion en flammes. Le malheureux pilote sera finalement tué lorsque le convoi de l'ambulance dans laquelle il se trouvait fut décimé par la chasse alliée lors de la retraite par la vallée du Rhône ainsi, et malgré le fait que Robert Heichele ait effectivement existé, la piste "du vainqueur probable de Saint-Exupéry" sera définitivement écartée par la suite, car provenant de l'imagination pure et simple d'un passionné allemand qui s'excusera peu après par courrier d'avoir laissé son fantasme il aurait été une connaissance du pilote Heichele devenir officiellement une "réalité".
Gourmette de Saint-Exupéry retrouvée en 1998.
Dans les années 1990, un autre témoignage surgit tardivement, à propos d'une habitante de Carqueiranne, madame Simone Boudet, qui aurait vu, le jour fatidique, le Lightning se faire abattre. La mer aurait ensuite rejeté le corps d'un soldat sur la plage, lequel aurait été enterré anonymement dans le cimetière de la commune. Était-ce Saint-Exupéry ? Pour le savoir, il faudrait exhumer le corps, procéder à des comparaisons avec l'ADN des membres de sa famille, lesquels s'y montrent opposés. Mais... là aussi, et d'après les anciens du pays, il fut avancé que les débris de vêtements militaires, toujours portés par la dépouille, étaient d’origine allemande. Il faut aussi savoir qu'au moins trois épaves d'avions de guerre allemands reposent dans la baie à plus ou moins grandes profondeurs. Chaque fois, ces révélations relancent l'intérêt aussi bien des spécialistes que du grand public, pour le mystère Saint-Ex.
Enfin, en 2000, des morceaux de son appareil, soit une jambe du train d'atterrissage gauche, des éléments de carlingue partie gauche d'une des deux poutres de cet avion aux lignes très particulières sont retrouvés en Méditerranée au large de Marseille, face nord-est de l'ïle de Riou archipel du même nom par le plongeur professionnel marseillais Luc Vanrell. Deux années plus tôt, le 7 septembre 1998, un patron pêcheur marseillais, Jean-Claude Bianco, assisté de son second, le marin Habib Benhamor, avait fortuitement remonté dans ses filets une gourmette en argent oxydée par un long séjour sous-marin et sur laquelle était gravée l'identité d'Antoine de Saint-Exupéry. Il devenait évident que la zone de disparition du commandant de Saint-Exupéry avait été localisée. Remontés à la surface entre le 1er et le 3 septembre 2003, les vestiges de l'avion tant recherché sont formellement identifiés, le samedi 27 septembre 2003, par l'association Aéro-Re.L.I.C. équipe composée de Philippe Castellano, Brian Cyvoct et Christian Vigne grâce à un numéro matricule retrouvé gravé par le constructeur Lockheed, Californie de l'appareil. Les pièces du Lightning F-5B # 42-69223 sont désormais exposées au Musée de l'air et de l'espace du Bourget, dans un espace consacré à l'écrivain aviateur.
-5 Lightning à bord duquel Antoine de Saint-Exupéry a disparu le 31 juillet 1944.
Mais rien ne permet de conclure définitivement sur les circonstances de sa mort, malgré la simulation informatique de l’accident – à partir des pièces déformées – qui montre un piqué, presque à la verticale et à grande vitesse, dans l’eau. Est-elle la conséquence d'une énième panne technique, d'un malaise du pilote ? Certains avancent même, au grand dam de ses proches, l'hypothèse du suicide d'un Saint-Exupéry diminué physiquement il ne pouvait fermer seul la verrière de son appareil, désespéré par le monde qu'il voyait s'annoncer, thèse confortée par certains de ses derniers écrits, au ton franchement pessimiste, par exemple les dernières lignes d’une lettre adressée à Pierre Dalloz, écrite la veille de sa mort :
Si je suis descendu, je ne regretterai absolument rien. La termitière future m’épouvante. Et je hais leur vertu de robots. Moi, j’étais fait pour être jardinier.
Île de Mainau, lac de Constance, Allemagne.
Être homme, c'est précisément être responsable.
Mais, en mars 2008, un ancien pilote de la Luftwaffe, sur Messerschmitt Bf 109, Horst Rippert, affirme dans le journal La Provence avoir abattu un avion de type P-38 lightning, le 31 juillet 1944, dans la zone où se trouvait Saint-Exupéry. En mission pour retrouver un avion ennemi qui survolait la région d'Annecy, Horst Rippert tourna plusieurs minutes au-dessus de la Méditerranée sans rien repérer. Soudain, un avion allié le croisa, 3 000 mètres au-dessous de lui. Horst Rippert tira et toucha. L'avion s'enflamma et tomba à pic dans la Méditerranée. Saint-Exupéry fut porté disparu ce jour-là, donnant lieu au mystère sur sa disparition. Si j'avais su qui était assis dans l'avion, je n'aurais pas tiré. Pas sur cet homme, déclara Horst Rippert, qui admirait l'écrivain. Thèse cependant mise à mal par bien des incohérences. Après la guerre Horst Rippert, frère d'Ivan Rebroff décédé en février 2008, soit peu avant cette révélation, s'était reconverti dans le journalisme et dirigeait le service des sports de la ZDF.
Ses œuvres
Si elles ne sont pas tout à fait autobiographiques, ses œuvres sont largement inspirées de sa vie de pilote aéropostal, y compris pour Le Petit Prince 1943 — sans doute son succès le plus populaire il s'est vendu depuis à plus de 134 millions d'exemplaires dans le monde, et se trouve être donc le second ouvrage le plus vendu au monde après la Bible — qui est plutôt un conte poétique et philosophique.
Il a écrit d'autres livres, tout aussi connus : Courrier Sud 1929, Vol de nuit 1931, Terre des hommes 1939, Pilote de guerre 1942, Lettre à un otage 1944, Écrits de guerre rassemblés en 1982, et Citadelle posthume, 1948. Tous ses romans racontaient l'histoire de ses voyages sous forme de fiction et dans la fantaisie.
L'Aviateur
Publié en 1926. Le premier texte édité de Saint-Exupéry, fragment semble-t-il d'un ensemble plus vaste, et qui servira de matériau pour Courrier sud.
Courrier sud
Publié en 1929. À travers le personnage de Jacques Bernis, Saint-Exupéry raconte sa propre vie et ses propres émotions de pilote. Louise de Vilmorin est campée dans le personnage de Geneviève.
Vol de nuit
Publié en décembre 1931. Cette œuvre qui atteint au dépouillement de la tragédie, est préfacée par son ami André Gide, valut le prix Femina à Antoine de Saint-Exupéry et le consacra comme homme de lettres. Ce fut un immense succès qui a donné lieu à de multiples traductions. Son adaptation cinématographique fut même vendue à Hollywood.
Le personnage principal, Rivière, est inspiré par son chef Didier Daurat. Il donne vie à un chef qui sait pousser ses hommes au bout d'eux-mêmes pour la réalisation de leur mission : le courrier doit passer à tout prix, la mission dépasse en valeur la vie humaine. Les valeurs que le roman véhicule sont : primauté de la mission, importance du devoir et responsabilité de la tâche à accomplir jusqu'au sacrifice.
Terre des hommes
Publié en décembre 1939, il obtient le Grand prix du roman de l'Académie française. C'est une suite de récits, de témoignages et de méditations à partir de la somme d'expériences, d'émotions et de souvenirs qu'il a accumulés lors de ses nombreux voyages. C'est aussi un hommage à l'amitié et à ses amis Mermoz et Guillaumet et plus largement une vision romantique sur la noblesse de l'humanisme.
Pilote de guerre
Publié en 1942.
Le Petit Prince
Écrit à Eaton's Neck Northport, États-Unis et publié en 1943 à New York chez Reynal & Hitchcock en deux versions anglaise et française. Il ne sera publié en France qu'en 1946, soit deux ans après sa mort.
Un pilote, sans doute postal, s'est posé en panne dans un désert. Il y fait une rencontre à la fois tendre et surprenante.
Pour des raisons techniques, les aquarelles de l'auteur reproduites dans les versions françaises qui ont suivi n'étaient que des retramages de l'édition américaine, ce qui induisait une perte de qualité sensible. De plus, certains dessins avaient été modifiés de façon mineure. L'édition Gallimard parue en 1999 semble être la première à fournir des illustrations conformes à l'édition originale, de bien meilleure qualité technique et artistique en dépit d'un format plus réduit les techniques d'impression ayant elles aussi fait des progrès depuis 1943.
Lettre à un otage
Publié en 1944.
Citadelle
Publié en 1948. Commencée en 1936, cette œuvre ne fut pas achevée par Saint-Exupéry. Publiée dans une première version en 1948 à partir d'un texte dactylographié, elle ne comportait pas l'intégralité de la pensée de l'auteur. La totalité des manuscrits fut mise à la disposition des éditeurs en 1958 et permit de mieux épouser ses intentions. Citadelle n'est pas une œuvre achevée. Dans la pensée de l'auteur elle devait être élaguée et remaniée selon un plan rigoureux qui, dans l'état actuel, se reconstitue difficilement. L'auteur a souvent repris les mêmes thèmes, soit pour les exprimer avec plus de précision, soit pour les éclairer d'une de ses images dont il a le secret Simone de Saint-Exupéry.
Lettres de jeunesse 1923-1931
Publié en 1953. Nouvelle édition en 1976 sous le titre Lettres de jeunesse à l'amie inventée.
Carnets
Publié en 1953. Édition intégrale en 1975. Ensemble de notes tenu de 1935 à 1940 sur un agenda et cinq carnets. Très éclectique, il reflète les intérêts et curiosités de l'écrivain pour les sciences, la religion, la littérature et donne lieu à des réflexions et à des aphorismes pertinents.
Lettres à sa mère
Publié en 1955. Recueil de la correspondance de Saint-Exupéry avec sa mère couvrant la période 1910 - 1944.
Un sens à la vie, publié en 1956. Écrits.
Écrits de guerre 1939-1944, publié en 1982. Ce recueil posthume est préfacé par Raymond Aron.
Manon, danseuse
Publié en 2007. Court roman achevé en 1925. C'est l'histoire d'amour entre une poule, Manon, et un homme de quarante ans, grave, triste, qui cherche un sens à sa vie. Dès leur rencontre, se noue entre eux une relation amoureuse, l'homme protégeant tendrement sa pauvre petite fille, qu'il croit danseuse. Ils font l'amour sans passion. Partent en voyage en voiture. Mais il apprend un jour par trois de ses clients que Manon est en fait une prostituée. Ils rompent puis se revoient. Manon se jette sous les roues d'un camion et manque de mourir. Elle restera boiteuse.
Lettres à l'inconnue
Collection de lettres d'amour à une jeune ambulancière de la Croix-Rouge rencontrée en mai 1943 dans un train entre Oran et Alger. Ces lettres sont ornées de dessins du Petit Prince que Saint-Exupéry fait parler à sa place. Elles ont été mises au jour en novembre 2007 lors d'une vente publique, et publiées par Gallimard en septembre 2008 sous forme de fac-similés accompagnés de transcriptions.
Écrits de circonstances
« La Paix ou la guerre » 1938 pour Paris-Soir
« Moscou » 1935 pour Paris-Soir
« L'Espagne ensanglantée » août 1936 pour L'Intransigeant
« Le Vol brisé. Prison de sable » janvier-février 1936 pour L'Intransigeant
« Madrid » juillet 1937 pour Paris-Soir
Cinéma
Scénario original pour Anne-Marie, film français réalisé par Raymond Bernard, sorti en 1936.
Anecdote
Citations, etc., peuvent être inopportunes dans les articles (indiquez la date de pose grâce au paramètre date.
Il avait multiplié les défis, comme l'aviation, cultivé les amitiés les plus improbables et tenté d'apprivoiser des animaux sauvages : renard des sables, gazelle, caméléon, bébé phoque, puma, lionceau, qu'il embarquait parfois dans son avion, au grand dam de ses mécaniciens - l'un d'eux finira à l'hôpital, après l'épisode du lionceau.
Élève très moyen, Saint-Exupéry échoue à l'examen d'entrée de l'École navale, et c'est par dépit qu'il fera son service militaire dans l'aviation.
Saint-Exupéry fut le seul pilote étranger autorisé à monter à bord de l'avion géant soviétique Tupolev ANT-20 Maxime Gorki.
Il a aussi été un homme de sciences : il détient près d'une dizaine de brevets d'inventions techniques, et a aussi mis au point de nombreux problèmes mathématiques, dont le problème du Pharaon publié à son retour d'Égypte.
Lors de l'émission du billet de 50 francs français à l'effigie d'Antoine de Saint-Exupéry, la Banque de France avait commis une coquille en typographiant le nom Antoine de Saint-Éxupéry sur le billet.
Orson Welles avait acheté les droits du Petit Prince et avait proposé à Walt Disney de l'adapter en animation. Après l'avoir lu, Disney a dit qu'il n'y avait pas de place pour deux génies dans l'entreprise.
La grande maison de Charles De Koninck du Vieux-Québec, au 25 de la rue Sainte-Geneviève, classée depuis monument historique était un lieu de fréquentation des personnalités des mondes universitaire, scientifique, intellectuel et politique. Saint-Exupéry visita les De Koninck en 1942. Son fils, Thomas De Koninck était alors âgé de huit ans. Ce dernier a conservé les bribes de quelques moments vécus avec Saint-Exupéry : Un grand gaillard. C'était l'aviateur. Un bonhomme attachant, qui s'intéressait à nous, les enfants. Il nous faisait des avions en papier, des dessins. […] Il aimait les énigmes mathématiques. L'année suivante, Saint-Exupéry publiait Le Petit Prince. Selon la légende locale, Saint-Exupéry se serait inspiré du petit De Koninck, qui avait les cheveux blonds bouclés et posait beaucoup de questions. M. De Koninck refuse cependant cette interprétation : Le Petit Prince, c'est Saint-Exupéry lui-même.
Le 29 juin 2010, 110 ans exactement après sa naissance, les internautes se rendant sur le site Google.fr ont pu voir que le logo était décoré avec une illustration du Petit Prince.
Une notoriété mondiale
Sa ville natale de Lyon, en hommage à l'écrivain et en clin d'œil au pionnier de l'aéropostale, a rebaptisé l'aéroport de Satolas en aéroport international Lyon Saint-Exupéry et la gare de Lyon-Saint-Exupéry TGV.
Inscription au Panthéon de Paris.
Sur les murs du Panthéon de Paris, une inscription honore sa mémoire en ces termes :
À LA MÉMOIRE DE
ANTOINE DE SAINT EXUPERY
POÈTE ROMANCIER AVIATEUR
DISPARU AU COURS D’UNE MISSION
DE RECONNAISSANCE AÉRIENNE
LE 31 JUILLET 1944
Ont été nommés d'après lui :
des rues de plusieurs villes, dont Lyon et plusieurs villes de sa banlieue, Avignon, Brest, Romans, Laon, La Seyne sur Mer, Fribourg Suisse, Montréal
l’avenue Saint-Exupéry à Toulouse, qui mène à Montaudran où se trouvaient l'aérodrome de l'Aéropostale et les ateliers Latécoère. Une fresque 3mx10m à son effigie, y a été dessinée en 2010.
la place du Petit Prince, ainsi que l'école du Petit Prince, ornées d'une statue, se situent à Péchabou, en banlieue toulousaine.
la rue Saint-Exupéry au Mans où se situe le collège où il a étudié.
le quai Saint-Exupéry à Paris
le boulevard Antoine-de-Saint-Exupéry à Lyon
l’Espace Saint-Exupéry à Franconville
la place Saint-Exupéry à Cabris, où habitait sa mère
la quarante-quatrième promotion de commissaires de police issue de l’École nationale supérieure de la Police, entrée en fonction en 1994
le thème de l’Exposition internationale de 1967 à Montréal était Terre des hommes'.
de très nombreux établissements scolaires partout en France une trentaine rien qu'en Île-de-France, Saint-Dizier… et à l’étranger : lycée Antoine-de-Saint-Exupéry de l’Alliance française à Santiago du Chili, le collège Saint-Exupéry à Rabat, lycée français Saint-Exupéry à Ouagadougou, lycée Antoine-de-Saint-Exupéry à Hambourg, école Saint-Exupéry à Madrid, école française Saint-Exupéry à Kigali Rwanda…
des cinémas à Marignane et à Strasbourg
des restaurants, des bibliothèques
un sommet argentin l’aiguille Saint-Exupéry, 2 558 m, à proximité de mont Fitz Roy, près de d’El Chaltén, province de Santa Cruz. La face sud du pic s'appelle Le Petit Prince. La face Est de l'aiguille Guillaumet voisine 2 579 m s'appelle Terre des hommes. Le pilier Est de l'aiguille Mermoz également voisine 2 732 m s'appelle Vol de Nuit et sa face nord-ouest Hyper-Mermoz. Le petit prince est dessiné se tenant au sommet du cerro Fitz Roy au chapitre XX du Petit Prince
la première promotion du Collège d'Europe à Bruges
l’aéroport de Lyon-Saint-Exupéry, a été renommé le 29 juin 2000 à l’occasion du centième anniversaire d’Antoine de Saint-Exupéry né à Lyon
la vingtième promotion de l'Institut Méditerranéen d'Étude et de Recherche en Informatique et Robotique IMERIR à Perpignan
L'institut de recherche technologique IRT de Toulouse dans le domaine de l'aéronautique a été nommé IRT Saint Exupéry.
2578 Saint-Exupéry, astéroïde.
Billet de 50 francs
Jardin royal de Toulouse
Il a été représenté par différents artistes :
La Banque de France a émis des billets de banque d'une valeur de 50 francs environ 7,6 € à son effigie entre 1996 et 2002.
Plusieurs timbres-poste ont été imprimés en l'honneur de Saint-Exupéry, notamment :
AOF : Poste aérienne valeur faciale 8 F, de 1947 ;
Cameroun : valeur faciale 60 F, de 1977 ;
France : Poste aérienne valeur faciale 50 F, émis le 18 janvier 1948, dessiné et gravé par Pierre Gandon ;
France : Poste aérienne valeur faciale 20,00 de 1970 en médaillon avec Jean Mermoz, dessiné et gravé par Jean Pheulpin;
France : Poste aérienne valeur faciale 3,00F/0,46 € émis le 26 juin 2000 pour le centenaire de sa naissance ;
France : feuillet de timbres édité en 1998 sur le thème du Petit Prince.
Une statue d'Antoine de Saint-Exupéry et du petit prince, œuvre de Christiane Guillaubey, est exposée sur la place Bellecour à Lyon.
Il existe une statue en son hommage à Toulouse, au centre du Jardin Royal.
Un buste de Saint-Exupéry, œuvre de Madeleine de Tézenas, sculpteur et peintre de l'air, est exposé au square Santiago-du-Chili à Paris.
Une statue du petit prince a été inaugurée le samedi 16 septembre 2006 à Northport États-Unis, la bourgade où il rédigea en 1942-1943 dans la maison Bevin House du quartier Eaton's Neck Le Petit Prince. C'est une œuvre de Winifred S. DeWitt Gantz. La statue se trouve dans la cour de la bibliothèque publique de Northport, 151 Laurel Avenue, NY 11768.
Sur une place d'Agay, où habitait sa sœur Gabrielle, une fontaine est dédiée au petit prince.
La monnaie de Paris a frappé un presse-papier, une médaille, un bracelet et fondu une statuette de 22 cm à l'effigie du petit prince.
Un hommage collectif aux aviateurs français pionniers de l'Aéropostale, dont il fait partie, figure dans une stèle à l'aéroport Jorge Newbery de la ville de Buenos Aires, près du musée de l'Aviation argentin.
Un téléfilm, Saint-Exupéry : La Dernière Mission, réalisé en 1994 pour France 3 par Robert Enrico retrace sa vie film réédité en 2009 au format DVD.
La fondation Antoine de Saint-Exupéry pour la Jeunesse a été créée en 2009 sous l'égide de la Fondation de France par les héritiers d'Antoine de Saint-Exupéry. Elle soutient des projets tournés vers la jeunesse, en France et dans le monde, portant les valeurs d'Antoine de Saint-Exupéry35. Elle a notamment soutenu la formation de jeunes apprentis mécaniciens aéronautiques.
Les papiers personnels d'Antoine de Saint-Exupéry sont conservés aux Archives nationales sous la cote 153AP.  
Posté le : 29/07/2016 19:23
|
|
|
|
|
André Citroén |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Le 3 juillet 1935 à Paris 16e meurt André Citroën
il a alors 57 ans né le 5 février 1878 à Paris 9e au 44, rue Laffitte, ingénieur polytechnicien français, pionnier de l'industrie automobile, fondateur de l'empire industriel automobile de même nom en 1919.
C'est l'une des figures les plus importantes de l’industrie automobile. Son œuvre dépasse les frontières françaises, tant les méthodes de production et de marketing à grande échelle qu'il introduisit ont révolutionné le domaine. L’Amérique où s’invente la production moderne de l’automobile est devenue la référence d’André Citroën. Il désire être le Henry Ford européen, appliquant les méthodes du fordisme ajoutées à l’exigence et l’innovation technique, et construire une voiture populaire pour mettre l’automobile à la portée du plus grand nombre.
André Citroën ne s'est pas fait connaître comme ingénieur automobile, mais en tant qu'industriel. Sa gestion de l'entreprise et son charisme plus que son génie de l'invention lui ont permis de s'entourer de grands noms et de talents de l'époque. Il a su les motiver grâce à un entregent hors pair. Il a également su apporter les techniques développées en Europe, notamment de l'Allemagne, et d'outre-Atlantique. André Citroën n'a pas plus inventé la traction avant qu’il n’a été le premier à avoir commercialisé une voiture dotée de cette technique ; mais la firme met au point un joint homocinétique plus simple et plus fiable que ses prédécesseurs. Les Citroën 7, 11 et 15 traction avant restent les premières automobiles à avoir popularisé cette technique, au point d'être devenues dans le langage courant les Tractions . Il est également réputé pour son savoir-faire médiatique, à l'image de la formidable campagne orchestrée lors du lancement de la Traction Avant. Le slogan En avant ! devient le symbole de la firme.
Malgré ces nombreuses qualités, le goût pour la démesure d'André Citroën et l'expansion trop rapide de sa firme mènent la société Citroën à la liquidation judiciaire, puis à sa reprise par Michelin pour éviter la faillite.
Il est fait drand officier de la Légion d'honneur en 1931.
En bref
Ancien élève de l'École polytechnique, André Citroën commence sa carrière de mécanicien et d'animateur — certains le qualifieront plus tard de joueur — en fondant à Paris, à l'âge de trente-cinq ans, la Société des engrenages Citroën pour l'exploitation d'un brevet polonais sur la taille des engrenages à denture en chevron. En l'espace de quatre ans, la petite entreprise voit ses ventes multipliées par dix et André Citroën sera sollicité par Škoda, qui veut exploiter son brevet en Europe centrale. Sa réputation d'organisateur commence à s'établir et la Société des autos Mors fait appel à lui pour réanimer l'entreprise ; la production annuelle de Mors passera de cent vingt-cinq à douze cents véhicules par an, en dépit de méthodes de production extrêmement artisanales — il est vrai qu'elles sont d'ailleurs communes à toute la construction automobile européenne de cette époque ; Citroën gardera le souvenir de son passage chez Mors lorsqu'il créera sa propre usine. En 1915, il s'engage envers le général Baquet, directeur de l'Artillerie, à construire une usine capable de produire 20 000 obus par jour et à en assurer l'approvisionnement en matières premières. En six semaines, l'usine du quai de Javel est construite sur l'emplacement d'anciens terrains maraîchers et sa production atteindra le double du chiffre initialement annoncé. Citroën reçoit dès lors la responsabilité de l'approvisionnement en charbon et en matières premières de toutes les usines travaillant pour la Défense nationale.
À la fin de la Première Guerre mondiale, Citroën peut enfin donner libre cours à son vieux rêve, celui de fabriquer une voiture populaire, véhicule qui n'existe pas encore en France et dont il est à peu près le seul à pressentir l'avenir. À partir des installations du quai de Javel, dont il garde la disposition et qui sont aisément reconvertibles dans une production civile, il lance en juin 1919 le modèle A, torpédo d'une puissance de 8 CV, dont la réalisation entière (bois, tôle, émail) sera effectuée à Javel et non plus dispersée entre des façonniers spécialisés. Ce modèle comporte un démarrage et un éclairage électriques, un volant à gauche et le symbole stylisé du double chevron polonais qui reste jusqu'aujourd'hui la marque de tous les véhicules de la firme. Après le type A de 1919, Citroën lance la B2 en 1921, la B10 en 1924 puis la B12 en 1925. La production de la firme passera de cent véhicules par jour en 1919 à trois cents véhicules en 1923. En 1922, la production des usines Citroën débordera du quai de Javel pour s'étendre à Clichy, Levallois, Saint-Ouen, tandis que les méthodes de Ford (construction en série, standardisation des pièces) sont appliquées aux ateliers du quai de Javel.
Cette période est également celle des grandes croisières Citroën, dont l'effet publicitaire sera énorme et qui, sur le plan technique, démontra la validité du véhicule « tout terrain » semi-chenille : traversée du Sahara de Touggourt à Tombouctou en 1922-1923 ; première traversée de l'Afrique de Colomb-Béchar à Tananarive en 1924 croisière Noire ; traversée de l'Asie de Beyrouth à Pékin par l'Himalaya et le désert de Gobi en 1931-1932 (croisière Jaune), au cours de laquelle le R.P. Teilhard de Chardin étudie la géologie des déserts de l'Asie centrale ; traversée de l'Amérique du Nord entre Chicago et l'Alaska en 1934 (croisière Blanche). C'est aussi l'époque des grandes illuminations de la place de la Concorde et de l'Arc de triomphe, offertes à la Ville de Paris, et de la publicité lumineuse sur la tour Eiffel en lettres de trente mètres de haut. Les initiatives de Citroën peuvent également être moins spectaculaires, sans pour autant cesser d'être originales et novatrices : application du système d'échange standard des moteurs, organisation des transports par cars dans des banlieues de plusieurs villes dont Paris, création d'une compagnie d'assurances à bas prix pour les clients de la firme, pose de panneaux de signalisation sur les routes. Par ailleurs, la notoriété de la firme s'étend et des filiales de Citroën sont constituées dans différents pays d'Europe (Allemagne, Angleterre, Espagne, Pologne, Suède). En 1928, la production de la firme s'élèvera à quatre cents voitures par jour, ce qui représente plus du tiers de la production française. Cependant, l'empire d'André Citroën est menacé et le nombre de ses ennemis et des créanciers de la firme s'accroît. À un moment où la dépression américaine envahit l'ancien continent et en une période de crise politique, tant française qu'européenne, Citroën lance la première automobile à traction avant qui lui vaudra jusqu'en 1947 la faveur du public, mais le place, en 1934, dans de graves difficultés financières.
Tout l'éclat dont fit preuve pendant quinze ans le fondateur de la firme et son amour du jeu dans tous les sens du terme se retournent contre lui. L'année même de la sortie de la traction avant, en 1934, la firme dut déposer son bilan et, sur l'ordre du gouvernement, son principal actionnaire, la Société des pneumatiques Michelin, reprit l'entreprise puis l'absorba. Abattu et malade, André Citroën meurt quelques mois plus tard, un an avant la première apparition de la 2 CV. Jean-Pierre LÉVIS
Sa vie
André Citroën est le cinquième et dernier enfant de Levie Bernard Citroen, un diamantaire juif néerlandais de 35 ans, émigré à Paris en 1873, et de Amalia Kleinmann, juive polonaise de 25 ans originaire de Varsovie.
Le nom Citroën possède toute une histoire. L'arrière-grand-père d'André, dénommé Roelof, est un marchand d'agrumes en Hollande. En 1810, lorsque Napoléon Ier annexe le Royaume de Hollande, les juifs néerlandais sont soumis au code Napoléon et doivent choisir un nom pour leur identification. Roelof choisit alors de se faire appeler Limoenman homme-citron, surnom que ses clients lui donnaient6. Son fils, Barend, ne prend pas la suite des affaires de Roelof et se tourne vers le négoce de joyaux, qui connaît un essor important au XIXe siècle. À la suite de ce nouveau statut social, Barend francise progressivement son nom, dans un premier temps en Limoenman-Citron puis en Citroen.
Les époux Citroen vivent dans un appartement du 9e arrondissement de Paris, au 44, rue Laffitte, puis après la naissance de leurs enfants et l'accès à un certain niveau de vie, dans la rue de Châteaudun. En 1884, son père se suicide en se jetant par la fenêtre, alors qu'André n'a que six ans, après s'être lancé dans une spéculation à hauts risques dans une mine de diamant en Afrique du Sud. Les actions se révélèrent sans aucune valeur. La famille n'est pas ruinée, mais la banqueroute pèse sur les épaules de Lévie. Une première tentative de suicide avait échoué. Surveillé depuis par les siens, il réussit néanmoins à déjouer cette surveillance le 16 septembre 1884 à 3 h du matin ; il se brise les cuisses et la colonne vertébrale, et meurt le matin malgré les soins du médecin de quartier. André et ses aînés sont alors élevés par leur mère qui reprend le négoce de diamants et de perles fines. Après cette tragédie, la famille Citroën, s'installe au 62, rue La Fayette, où les enfants reçoivent une éducation totalement française, de sorte qu'ils se sentent citoyens français à part entière.
André entre au lycée Condorcet, sous le nom Citroën. C'est la première fois qu'un tréma apparaît sur le e, André remplissant ses papiers avec cette nouvelle graphie car il n'aime pas entendre prononcer le son /ɑ̃/ de la fin de son nom10. Il se révèle vite brillant élève, particulièrement pour les sciences et les techniques. Âgé de 9 ans, il découvre l’œuvre visionnaire avant-gardiste de Jules Verne qui l'inspirera toute sa vie. La construction de la tour Eiffel pour l'exposition universelle de 1889 l'incite à devenir ingénieur et industriel et à participer aux futurs grands défis industriels du vingtième siècle. En octobre 1898, il intègre l'École polytechnique4 au 62e rang sur les 201 admis. Son rang de sortie 162e sur 192 élèves ne lui permet pas d'envisager une carrière au service de l'État ou d'un grand corps, ce qui néanmoins lui convient.
Débuts d'une vocation
Engrenages à doubles chevrons en V
Engrenages à chevrons en V devenu emblème et logo de Citroën
En 1900, pour les vacances de Pâques, André Citroën rend visite à de la famille en Pologne et rencontre son beau-frère dont l'un des clients — petite firme mécanique — a mis au point un procédé d'engrenages aux dents taillées en V. À partir de modèles en bois, ces engrenages sont moulés dans des moules en sable et utilisés à moindre coût pour des minoteries et dans des usines de filature. André Citroën voit dans cette découverte le moyen de lancer sa carrière indépendante d'industriel et propose d'acheter la licence du procédé de fabrication à ce moment-là détenu par les Russes.
Cette conception technique innovante permet de transmettre des puissances importantes tout en ayant un fort rapport de réduction de l'arbre de sortie. Les engrenages à denture hélicoïdale contribuent à un contact prolongé des dents pendant l'engrenage et, qualité importante à l'époque, assurent un plus grand silence durant le fonctionnement par rapport aux engrenages à taille droite, grâce à un frottement plus faible. L'inconvénient est que cela induit des efforts axiaux importants dans les paliers. La double denture en chevrons offre entre eux un contact dans les deux sens, ce qui compense l'effort axial. Cependant, pour obtenir un tel fonctionnement, il est nécessaire que les dents soient parfaitement usinées. La petite firme polonaise ne peut se permettre une telle précision de fabrication, ni même d'ailleurs les grandes entreprises de fabrication en Europe. André Citroën se tourne alors vers l'Amérique, où les constructeurs de machines-outils ont une avance certaine. De retour en France, aidé financièrement par le banquier Bronislaus Goldfeder, il transpose l'idée avec des chevrons en acier et met au point, par ailleurs, une fraiseuse équipée d'un outil de coupe profilé capable de traverser le billot d'acier de part en part à un régime de 2 000 tr/min, atteignant ainsi la précision d'usinage requise.
C'est le début de l'une des plus grandes aventures industrielles des temps modernes. Avant de pouvoir réellement s'occuper de sa trouvaille et commencer la production du nouveau système, Citroën doit terminer sa dernière année d'étude à l'école Polytechnique ainsi que ses années de service militaire, obligatoire à cette époque. Il passe ainsi deux ans dans le 31e régiment d'artillerie du Mans, avec le grade de sous-lieutenant.
Automobiles Mors
Appelé au chevet de la société automobile Mors en difficulté, pourtant célèbre pour avoir battu au début du siècle des records de vitesse, il participe à son redressement entre 1906 et 1914, lui permettant de décupler son chiffre d'affaires. Il est ainsi nommé directeur général administrateur de l'entreprise par les frères Émile et Louis Mors. Il réorganise l'étude des besoins clientèle, la gestion, modernise, crée de nouveaux modèles et double la production de la marque en 10 ans. L'entreprise produit 300 automobiles en 1908, pour atteindre 800 unités en 1913.
André Citroën est un découvreur de talents et un organisateur de génie. Il n'est ni inventeur, ni technicien. Il se passionne pour la fabrication et la distribution à grande échelle. En 1912, dans le cadre de son travail pour les usines Mors, André Citroën effectue son premier voyage aux États-Unis, voyage qui marquera profondément sa vie et sa carrière. Il visite l'usine Ford d'Henry Ford à Dearborn près de Détroit, dans laquelle est appliqué le taylorisme, devenu fordisme. Il s'agit de la démocratisation de biens de production industrielle fabriqués en grande série à moindre coût de revient. Sa visite lui permet de s'imprégner des méthodes appliquées dans les usines américaines.
La direction des usines Mors permet à Citroën d'acquérir une certaine expérience, notamment dans les domaines humains. En effet, les conditions de travail des ouvriers à cette époque sont rudes, ce qui les amène en 1912 à se mettre en grève, pour l'adoption de la semaine anglaise des cinq jours. Citroën sait se montrer ouvert afin d'éviter toute confrontation inutile, et améliore ainsi les conditions de vie des travailleurs, et partant, leur efficacité. C'est dans cette entreprise qu'André Citroën va tisser de nombreux réseaux d'experts et de conseillers.
Citroën, Hinstin et Cie
En 1912, âgé de 35 ans, il s'associe avec André Boas et Paul Hinstin, qu'il connaît depuis le lycée Condorcet, avec qui il investit une grande partie de l'héritage de ses parents pour fonder la société Citroën, Hinstin et Cie, entreprise de fabrication d'engrenages, en particulier ceux à chevrons en V, avec une dizaine d'ouvriers dans le faubourg Saint-Denis du 10e arrondissement de Paris. Il emménage rapidement au 31, quai de Grenelle dans le 15e arrondissement de Paris à côté de l'usine des frères Mors, près du quai de Javel et se rebaptise Société anonyme des engrenages Citroën. Le logo de cette marque n'est autre qu'un double V renversé. André Citroën fonde sa réputation et sa fortune dans la production de ces engrenages. En effet, l'adoption de moteurs électriques pour l'alimentation des machines dans les industries nécessite des engrenages robustes, capables de réduire les hauts régimes fournis par ces moteurs, ce qui correspond parfaitement aux engrenages de Citroën. André Citroën dépose ainsi de nombreux brevets pour les applications de ses engrenages dans divers domaines comme les transmissions industrielles ou pour les trains arrière des automobiles.
Il est dans un premier temps à la fois ingénieur en chef, directeur de production, directeur commercial, étant donné que ses deux associés ont déjà d'autres engagements. Il devient également Président de la Chambre syndicale de l'automobile. En l'espace de quatre ans, la petite entreprise voit ses ventes multipliées par dix et André Citroën sera sollicité par Škoda, qui veut exploiter son brevet en Europe centrale.
Vie d'un grand industriel Jeux d'argent
La vie d'André Citroën devient vite aisée. Il vit avec son frère Bernard, au 21, rue d'Aumale dans le 9e arrondissement de Paris.
Bernard est un musicien amateur, entouré d'un groupe d'amis mélomanes, dilettantes et fortunés. André est donc souvent entouré de la gent féminine et participe à de nombreuses réceptions mondaines. C'est à cette époque, on l'imagine, qu'André Citroën développe son goût pour les jeux d'argent. Paris est une ville où les gens fortunés peuvent s'adonner à tous les plaisirs. Citroën développe ainsi un goût particulier pour la vie nocturne et mondaine. L'acquisition d'un certain statut social ainsi que d'une certaine fortune ne calme pas son goût immodéré pour les jeux d'argent. Il devient rapidement un habitué des tables de casino et des champs de courses tel que Longchamp. Perdant ou gagnant des sommes extraordinaires dans les casinos, notamment celui de Deauville, Citroën est réputé pour sa générosité. Il offre une voiture sans hésitation, aussi bien pour le petit personnel comme ses croupiers que pour des personnes plus aisées.
Vie privée
Bien que sa vie soit plutôt aisée, sa vie demeure sans excès (excepté pour le jeu. Il n'est pas intéressé par l'accumulation de biens, ne possède pas, contrairement à nombre d'industriels, de collections de tableaux, de yachts ou de grandes demeures. Ses possessions terriennes se limitent à ses usines, et sa résidence est louée. Outre les jeux, André Citroën a une réelle passion pour la musique. Il aime se rendre à l'opéra ou encore organiser des concerts particuliers pour sa famille.
C'est au cours d'une soirée dans un casino du Touquet, à l'automne 1913, qu'André Citroën rencontre Georgina Bingen 1892-1955, une jeune femme qui passe quelques jours de vacances avec ses parents. Le 27 mai 1914, deux mois avant la déclaration de la Première Guerre mondiale, il l'épouse1 dans la tradition et le couple aura une famille de quatre enfants.
André Citroën est souvent pris à tort pour un « play-boy », alors qu'il adore ses enfants et sa femme, et aime les emmener en vacances à la mer ou à la montagne.
La contribution à l'effort de guerre
Canon et munitions sur le terrain en 1915.
Sitôt la guerre déclarée, André est mobilisé en août 1914 en tant que lieutenant puis capitaine au 2e régiment d'artillerie de Metz. Sur la frontière Est où a lieu le conflit, il a l'occasion de constater le manque d'artillerie et de munitions face à l'artillerie allemande. À la suite de la mort de son frère Bernard sur le front, André Citroën est décidé, non seulement de faire son devoir, mais également de repousser l'ennemi le plus loin possible. En janvier 1915, il propose au général Louis Baquet, directeur de l'artillerie du Ministère de la Guerre, qui manque cruellement de munitions, d'appliquer le fordisme dans une usine construite en 3 mois, capable de produire 5 000 à 10 000 obus Shrapnel de type 75 par jour. Grâce à ses économies, celles de son bras droit Georges-Marie Haardt et surtout le financement d'un riche diamantaire d'origine arménienne, Atanik Eknayan qui avait déjà sauvé son affaire fragile de Mors, il fait ériger sur les 15 hectares de terrains vagues et de jardins potagers du quai de Javel, une immense usine ultramoderne et produit avec 13 000 ouvrières, 23 millions d'obus à raison de 10 000 par jour, à des cadences inédites pour l’époque. Il faut produire vite, bien, économiquement, pour mettre les produits fabriqués à la portée du plus grand nombre possible de consommateurs », dit-il. Le rythme imposé par ses usines est fatigant et de ce fait, André Citroën a pu parfois y être considéré comme un despote. Néanmoins, il est pourtant l'un des premiers industriels soucieux du bien être de ses ouvriers et évite d'imposer des tâches répétitives.
L'entreprise de munitions d'André Citroën est très vite réputée et devient un modèle d'organisation, d'efficacité et de responsabilité sociale. Les grandes personnalités aussi bien civiles que militaires visitent l'usine. Entre 1917 et 1918, le gouvernement le charge également de réorganiser le ravitaillement de l'industrie de l'armement, les services postaux militaires, et la distribution des tickets de ration de pain dans la région parisienne. Lorsque la guerre est terminée, André Citroën décide de reconvertir son usine du quai de Javel en usine de construction d'automobiles.
Fondation des Automobiles Citroën 1919
Sitôt la guerre terminée, l'essor de l'automobile est incroyable et les rues sont progressivement envahies de véhicules mus par leur propre énergie. En 1919, Les français produisent un nombre important d'automobiles, bien plus que les allemands ou les américains: Paris est la capitale de l'automobile dans le monde. Par ailleurs, les massacres des chevaux durant la guerre accélèrent la nécessité d'engins de traction efficaces.
Une Citroën Type A de 1921.
Lorsque l'Armistice de 1918 est signé, les usines Citroën perdent brutalement toutes leurs commandes de munitions. Néanmoins, Citroën s'est très tôt préparé à cet événement, en réinvestissant ses bénéfices dans une nouvelle entreprise : l'industrie automobile doit remplacer la production de munitions. André Citroën reconvertit ainsi son usine d'armement en industrie automobile en quatre mois, absorbant le constructeur automobile Mors et fonde Citroën avec pour emblème historique son double chevron en V.
Citroën a compris lors de son voyage aux États-Unis la nécessité de produire une automobile à grande échelle, c'est-à-dire avec une diffusion étendue au-delà des classes privilégiées. À l'image de la Ford T, la future Citroën se veut être à la fois outil de travail et objet de loisirs. En janvier 1919, André Citroën annonce ainsi à la presse française son intention de produire une automobile de grande série. Avec une annonce incroyable pour l'époque : la future automobile coûtera 7 250 francs, soit près de la moitié de la voiture la moins chère du marché. Cette campagne d'annonce est également historique sur un autre plan : C'est la première campagne de presse massive, qui provoque plus de 16 000 demandes de renseignements auprès de l'entreprise Citroën, et ce en deux semaines seulement28.
Assisté de son fidèle bras droit Georges-Marie Haardt pour la commercialisation, Citroën fabrique cette même année le premier modèle de la marque : la Citroën Type A pour la conception de laquelle il a recruté l'ingénieur Jules Salomon dès 1916. La première voiture européenne fabriquée en série à raison de 30 voitures par jour et 20 000 par an dès 1920N 6. Bien que le succès de Citroën soit sans précédent, le prix de lancement exceptionnellement bas pour l'époque, est obtenu au détriment du bénéfice nécessaire pour rembourser les lourds emprunts d’investissements.
En 1926, il conçoit avec l'aide de l'ingénieur américain Edward Gowan Budd, la Citroën B14, première voiture « d'Europe « tout acier » » dont la carrosserie solide est entièrement fermée. Une presse emboutit 400 longerons à l'heure, que l'on assemble par soudage avec le reste de la caisse12.
De 1928 à 1932 suivent les Citroën C4 et Citroën C6. Elles sont les premières Citroën à bénéficier d’un moteur flottant. André Citroën avait acheté la licence du brevet déposé par Chrysler après un voyage aux États-Unis.
En 1929, Citroën devient le second constructeur d'automobile mondial avec 400 véhicules par jour le tiers de la production française au détriment de l'équilibre budgétaire. De très graves problèmes de financement sont accentués par la Grande Dépression de 1929.
Pourtant, l'année 1929 se caractérise par le record de 102 891 automobiles produites, soit près du tiers de la production nationale. Un peu moins de la moitié des automobiles est exportée. Outre le quai de Javel, les usines Citroën s'installent à Suresnes, Clichy, Saint-Ouen, et Grenelle. On y emploie 32 000 ouvriers.
Des idées nouvelles
Publicité Citroën sur la tour Eiffel avec 250 000 ampoules.Service client et marketing
Citroën développe un véritable talent d'innovation pour mieux servir et fidéliser les clients. Citroën est le premier constructeur hors États-Unis, à proposer un manuel du conducteur avec chacun de ses modèles. Les garages sur lesquels l'emblème Citroën trône présentent, outre l'atelier, un hall d'exposition de modèles.
Un réseau de concessionnaires et de service après-vente doté de stocks de pièces détachées de grande ampleur et des solutions novatrices de crédit très avantageux installeront sa notoriété auprès du grand public. Outre un réseau commercial à grande échelle, André Citroën développe des compagnies de taxis et un réseau de transports ruraux Les cars Citroën. Les lois de l’exportation l’amènent à développer des sociétés en Belgique, aux Pays-Bas, en Allemagne, en Suisse, en Italie et au Danemark.
Pionnier de l'« ancêtre du marketing direct, André Citroën ouvre, dans ses usines, un département spécialisé chargé d'accumuler, à l'aide du réseau de concessionnaires, des informations sur les clients, comme leur nom, leur adresse, etc. En 1920, la S.O.V.A.C., première entreprise européenne de crédit à la consommation, est créée. Citroën est également connu pour être un bon promoteur, démontrant la qualité de ses automobiles en réalisant des essais de chocs avant la lettre.
Par la suite, un courrier est envoyé aux clients qui se sont rendus dans les concessions, les remerciant de leur visite et leur indiquant quel serait le modèle leur correspondant le mieux. La lettre imprimée en caractères d'imprimerie comporte une signature et une formule de politesse manuscrites, procurant ainsi la sensation aux destinataires, qu'André Citroën s'adresse personnellement à eux. La distribution chaque semaine dans toute la France de plusieurs milliers de lettres augmente spectaculairement les résultats de ventes. D'après les responsables de l'entreprise, 15 % des ventes sont le résultat de cette méthode.
Médiatisation
La notoriété d'André Citroën progresse rapidement dans le grand public grâce à l'action de son équipe, dirigée par Pierre Louÿs affichiste officiel puis directeur des services artistiques et photographiques et l’agence Wallace et Draeger10. Il innove en matière de publicité et de marketing de masse. C'est ainsi qu'il organise et assure la couverture médiatique, de décembre 1922 à février 1923, de la traversée du Sahara en autochenilles démontables Citroën-Kégresse tout-terrain. Puis celles des grandes croisières : Croisière noire en Afrique en 1924, Croisière jaune en Asie en 1931, et Croisière blanche en Alaska en 1934. De nombreuses pages de publicité paraissent dans la presse régionale et nationale. Des milliers d'autres sont affichées dans les rues.
L'esprit médiatique du très entreprenant André Citroën s'affranchit des limites traditionnelles :
Le 4 octobre 1922, lors de l'ouverture du 17e Mondial de l'automobile de Paris, un avion dessine en lettres de fumée blanche le nom de Citroën, au-dessus de l'Arc de Triomphe. Le nom fait ainsi 5 km de long.
En 1925, André Citroën fait installer sur la Tour Eiffel une énorme publicité lumineuse pour sa marque, s’étirant en hauteur. Les illuminations par 250 000 ampoules en six couleurs figurent neuf tableaux, le dernier étant le nom Citroën avec un lettrage stylisé version art déco. Elle est installée jusqu'en 1933 bien que la ville ait, depuis 1926, multiplié ses taxes par six.
L'histoire retient également l'arrivée de l'aviateur Lindbergh en approche du Bourget, après une longue traversée de l'Atlantique à bord du Spirit of Saint Louis, qui se servit de l'enseigne lumineuse Citroën de la tour Eiffel comme balise pour se repérer. André Citroën profite alors de l'événement et invite le héros national à une réception au quai de Javel, faisant une fois de plus, une incroyable publicité pour sa firme.
Fabrication
Par ailleurs, le concept de pièce détachée d'origine garantie voit le jour, permettant aux clients de pouvoir remplacer une pièce cassée, sans devoir attendre l'intervention d'un artisan. La qualité de fabrication des automobiles Citroën est l'un des points essentiels qui les caractérise à cette époque. Il met ainsi en place des laboratoires de contrôle de qualité, ces derniers prélevant des pièces au hasard dans les usines afin de vérifier leur conformité. De nombreux constructeurs considèrent à l'époque que leur travail est terminé dès lors qu'une voiture sortie des usines est vendue. Citroën est dans un point de vue totalement différent. Il explique même que dès qu'une vente est conclue, une autre au moins aussi importante commence. C'est sur la qualité du service après-vente dans lequel le client a déjà investi lors de son achat que se décidera son retour ou non dans les halls d'exposition pour changer de voiture.
Environnement de travail
Citroën est conscient qu'une organisation importante ne peut fonctionner sans la coopération du personnel. Il accorde d'autant plus d'importance au bien être et aux conditions de travail qu'en 1918 son effectif total de 11 700 salariés compte près de 6 000 femmes. Dans le hall de montage elles représentent plus de 90 % : 680 sur un total de 750 personnes. Des installations d'hygiène et des services sociaux -tout à fait exceptionnels pour l'époque- sont mis en place.
L'usine est un modèle de propreté, les ateliers sont bien éclaires et aérés. Quatre mille vestiaires individuels sont mis à disposition. Mille trois cents lavabos et deux cent cinquante WC jouxtent les ateliers. Des douches sont prévues pour les employés des ateliers les plus salissants. La tenue de travail comporte une blouse blanche et un bonnet de couleur par atelier.
Des distributions d'eau potable et de boissons chaudes sont organisées dans les ateliers. La cantine 3 000 m2 d'un seul tenant dessert 3 500 couverts. Le menu est identique pour les ouvriers, employés et cadres. Après le repas, ceux qui le veulent peuvent jouer au billard, aux cartes ou à divers jeux de société. Une salle de couture est prévue pour les dames.
L'infirmerie est dirigée à plein temps par un médecin entouré de 15 infirmières. Elle comporte salles d'attentes, salles d'examens médicaux, de radiographie, de gynécologie et de chirurgie. Les malades et accidentés graves sont immédiatement transférés à l’hôpital par l'ambulance de l'usine. Un cabinet dentaire ultra-moderne abrite 6 praticiens qui peuvent soigner jusqu'à 100 personnes par jour.
Toute ouvrière enceinte a droit à une prime mensuelle plus une prime de naissance, un mois de convalescence payé ainsi qu'à des primes d'allaitement.La pouponnière et la crèche sont installées au milieu d'un jardin dans les quatre étages d'une ancienne école.
La coopérative d'achats propose à prix réduits tout ce qu'on pouvait désirer acheter : Boucherie, crèmerie, épicerie, mais aussi articles de mode, chaussures et jouets...
Le samedi soir, des séances de cinéma sont organisées dans la grande salle du restaurant d'entreprise, où sont projetés des films commerciaux grand publics. Ces séances intègrent la projection de courts reportages cinématographiques sur les activités ou réalisations de l'entreprise.
Société Citroën-Kégresse-Hinstin
Autochenille Adolphe Kégresse
Le tsar Nicolas II de Russie est à l'origine de l'invention des autochenilles. Grand défenseur et passionné d'automobile, il en possède une importante collection pour l'époque, à l'image de sa Rolls-Royce Silver Ghost. Cependant, le rude et long hiver russe laisse peu de routes praticables, si bien que les voitures du tsar ne peuvent rouler que quelques mois par an. En 1905, Nicolas II fait alors appel à un ingénieur français, directeur technique du corps impérial des transports motorisés, Adolphe Kégresse, pour mettre au point un système permettant aux automobiles de se mouvoir sur la neige. Ce dernier imagine dès lors un système de chenillettes, amovibles et légères, qu'il fixe à la place des roues arrière.
À la chute du tsar, après la Révolution d'Octobre, Kégresse rentre en France. Il rencontre André Citroën en 1920, qui voit immédiatement le potentiel du système des chenilles et l'acquiert. Il fonde une société indépendante dénommée « Citroën-Kégresse-Hinstin, afin de pouvoir exploiter pleinement l'invention. Une automobile équipée des autochenilles sur une base de Citroën 10HP type B2 est mise au point33. André Citroën a bien compris l'importance stratégique de ce système dans les colonies d'Afrique et d'Orient. Il s'agit maintenant de la prouver aux autres pays en réalisant la traversée du Sahara.
La traversée du Sahara
À l'issue de la Première Guerre mondiale, le projet d'une liaison sûre et rapide entre la France métropolitaine et l'Afrique équatoriale séduit coloniaux et industriels, et trouve un écho très favorable dans les milieux militaires et scientifiques. Une grande idée que l'automobile rend enfin possible. Confiant dans son matériel, André Citroën est quant à lui persuadé que cette liaison peut se faire en 20 jours à peine.
André Citroën sait les difficultés technologiques que représente un raid en Afrique. Les véhicules ont de grandes difficultés à avancer dans le sable, les roues étant en permanence enlisées, et les écarts de température nuisent au moteur. Bouillants le jour, les liquides huile et eau gèlent la nuit.
Selon ses propres dires, La première idée d'un raid transsaharien naquit pendant la guerre 14-18 qui révéla l'importance des ressources des colonies d'Afrique équatoriale pour la France .... On réalise alors que ces richesses ne pourraient prendre leur vraie valeur qu'à partir de ... l'établissement d'un réseau efficace de communication.
Partis de Touggourt en Algérie, Georges-Marie Haardt, Louis Audoin-Dubreuil et une équipe de 10 personnes dont plusieurs militaires et un géographe, relient Tombouctou au Soudan, en 20 jours, comme l'espérait Citroën. Avec 5 véhicules Citroën à chenilles Kégresse, les membres de la « mission Haardt-Audouin effectuent la première liaison directe entre l'Algérie et l'Afrique Occidentale Française. Les 5 véhicules de l'expédition ont chacun un nom. Scarabée d'Or accueille Georges-Marie Haardt directeur des Usines Citroën, chef de mission et Maurice Billy pilote et mécanicien ; Croissant d'Argent, Louis Audouin-Dubreuil second chef de mission et Maurice Penaud pilote, mécanicien en chef ; Tortue Volante, Paul Castelnau géographe et cinéaste et Roger Prud'homme pilote, mécanicien ; Bœuf Apis, Georges Estienne lieutenant et Fernand Billy (pilote mécanicien ; René Rabaud pilote, mécanicien et l'adjudant Chapuis guide, interprète montent à bord de Chenille Rampante.C'est en grande pompe, le 7 janvier 1923 que le premier courrier transsaharien automobile est remis au commandant de la région de Tombouctou, le colonel Mangeot. André Citroën a su faire de cette expédition, une incroyable publicité pour sa firme. Il réitérera cette expérience de la Croisière noire en Afrique en 1924 puis organisera la Croisière jaune en Asie en 1931, et la Croisière blanche en Alaska en 1934.
Croisière jaune, Croisière noire et Croisière blanche.
La rénovation du site de Javel
En 1933, André Citroën est invité par son concurrent Louis Renault à visiter une nouvelle usine Renault. Afin de demeurer compétitif avec Renault, il accentue lourdement son surendettement et multiplie les acrobaties de gestion. Les critiques sont nombreuses, lorsqu'il fait bâtir la plus grande usine ultramoderne d'Europe sur le site rénové de Javel en 6 mois avril à septembre 1933.
Elle est dotée d'une cathédrale de verre et acier» capable de produire 1 000 voitures par jour. Le chantier est conduit par tranches de travaux simultanés, inspiré des principes de l'organisation à la chaîne. Le plan des nouvelles installations est en forme d'arêtes de poisson: les chaines auxiliaires apportent des éléments terminés à deux chaines principales centrales de deux cent cinquante mètres débouchant sur un immense hall de livraison.
Sur le quai, l'ancien bâtiment administratif est remplacé par un long bâtiment à façade monumentale avec un porche entièrement vitré de deux cotés permettant d'avoir une longue perspective du hall de livraison et du montage. L'inauguration grandiose a lieu le dimanche 8 octobre 1933 : un banquet réunit dans le hall des livraisons 6 333 convives...
Avec la nouvelle usine de Javel, Citroën dispose d'un outil de production moderne, efficace et ultra-performant. Mais il allait lui falloir amortir les sommes importantes qu'avaient coûtées cette reconstruction.
Problème d'endettement chronique
La Citroën Traction Avant.
André Citroën est davantage un expansionniste qu'un comptable. En réalité, la firme Citroën connaît des problèmes financiers depuis sa création. Les bénéfices acquis lors de la production de munitions ne furent pas suffisants pour couvrir les investissements, 90 % des gains ayant été dépensés en taxes. La vente des premières automobiles a certes permis de soulager un temps la situation financière de Citroën, mais l'incessante et rapide croissance de la firme engendre de nombreuses dépenses qui épuisent ses ressources financières.
En mai 1934, un rapport publié par la Banque de France indique que la société Citroën accuse des pertes de 200 millions de francs38. Les banques perdent confiance, arrêtent de le suivre dans son surendettement chronique et confient à Pierre Michelin du groupe MichelinN 8, la gestion de Citroën avec la mission très difficile de lui éviter la faillite.
En 1933, André Citroën engage l'ingénieur André Lefebvre, ancien collaborateur chez Voisin et Renault. En un an, celui-ci conçoit et prépare la fabrication de la célèbre «Traction avant», qui est présentée aux concessionnaires le 24 mars 1934. Révolutionnaire à plus d'un titre, cette Traction Avant utilise des joints de transmissions homocinétiques inventé en 1926 par Pierre Fenaille et Jean-Albert Grégoire. Sa carrosserie est monocoque, autoporteuse et sans châssis. Son moteur chemisé est de type flottant comme celui des Rosalie. Par-dessus tout, elle offre une tenue de route qui deviendra légendaire. Mais le succès de ce modèle révolutionnaire, altéré par un manque de mise au point et des débuts techniques difficiles, ne suffit pas pour sauver le groupe de la faillite qui s'annonce.
Faillite, liquidation judiciaire et disparition
En raison de la crise que traverse l'Europe à cette époque, des conflits entre direction et ouvriers surgissent comme partout ailleurs. André Citroën, comme il l'a déjà fait auparavant, intervient personnellement, explique et négocie. En 1933, il est le premier à affronter des discussions tripartites patronat, ouvriers et syndicats. Au conflit de six semaines en 1933 et à la reconstruction complète de l'usine du quai de Javel se surajoutent des difficultés financières. André Citroën déploie alors une importante énergie, physique et morale, pour repousser les dates de ses créances, ce qui l'épuise énormément.
Malgré les propositions faites par Citroën et la Banque de France, les banques refusent tout compromis. Citroën sollicite alors Pierre-Étienne Flandin, président du Conseil mais ce dernier refuse toute intervention de l’État. Le 21 décembre 1934, Citroën est mise en liquidation judiciaire. Le gouvernement propose au principal créancier Michelin de reprendre la marque et de sauver les 250 000 emplois, de calmer 1 500 créanciers et des milliers de petits porteurs.
En 1935, âgé de 56 ans, André Citroën cède ses actions à Michelin et se retire en janvier, mais demeure le président du conseil d’administration, avant d'être remplacé en juillet par Pierre Michelin. Le 18 février, il est admis à la clinique Georges Bizet. Bien qu'opéré en mai, il meurt le 3 juillet de la même année d'un cancer de l'estomac après 15 ans d'activité industrielle au sommet. Enterré le 5 juillet, il repose au cimetière du Montparnasse.
En 1976, pour éviter une deuxième faillite, sur demande du gouvernement, Peugeot acquiert 90 % du capital Citroën à Michelin et devient jusqu'à ce jour le groupe PSA Peugeot Citroën, société à directoire et conseil de surveillance, propriété de la famille Peugeot.
Distinctions
Chevalier de la Légion d'honneur en 1923.
Officier de la Légion d'honneur en 1925.
Commandeur de la Légion. d'honneur en 1928.
Grand officier de la Légion d'honneur en 1931.
Hommage
En 1958, le quai de Javel, à Paris, est rebaptisé quai André-Citroën et l'usine historique, qui nécessitera huit ans pour sa démolition entre 1976 et 1984, laisse place au parc André-Citroën, en mémoire du chef d'entreprise que fut André Citroën. Un buste en bronze lui est consacré face à l'entrée du parc face à l'Hôpital européen Georges Pompidou.
Famille Citroën
Ses parents, Lévie Citroen et Amalia Kleinmann, ont eu cinq enfants, dont :
Jeanne Citroën 1872-1932, épouse de Bronislas Goldfeder
Hugo Citroën 1873-1953, époux de Suzanne Sarah Haarbleicher
Louis Hughes Citroën 1903-1944, polytechnicien, mort à Auschwitz
Fernande Citroën 1874-1963, épouse d'Alfred Lindon né Abner Lindenbaum , dont postérité :
Raymond Lindon, célèbre avocat et procureur des réquisitions des procès ayant suivi la Libération de la France
Jérôme Lindon 1925-2001, directeur des Éditions de Minuit de 1948 à 2001
Mathieu Lindon
Laurent Lindon
Vincent Lindon né en 1959, acteur, réalisateur et scénariste
Bernard Citroën 1875-1914
André Citroën 1878-1935.
Par sa femme Georgina Bingen, André Citroën est :
beau-frère de Jacques Bingen, grand résistant de la France libre.
André Citroën et Georgina Bingen ont été parents42 de quatre enfants :
Jacqueline Citroën 1915-1994, directrice de maison de haute couture, chevalier de la Légion d'honneur. Épouse de Paul de Saint-Sauveur, dont postérité :
André de Saint-Sauveur, père de trois enfants
Donine de Saint-Sauveur
Armand-Guillaume de Saint-Sauveur
Pauline de Saint-Sauveur
Bernard Maxime Citroën 1917-2002, ingénieur polytechnicien, résistant de la Seconde Guerre mondiale, commandeur de la Légion d'honneur, époux de Piroska Szabó 1919-1996 et père de trois enfants :
Henri-Jacques Citroën né en 1953, directeur et rédacteur en chef de Paris Caraïbes, président de Henri J. Citroën et associés, entreprise d'importation et de distribution de vins et spiritueux depuis 1996, président de la section Venezuela des Conseillers du Commerce extérieur de la France depuis 2009.
Charles-Henri Citroën
Clémentine Citroën
Anne-Rosalie Citroën
Philippe Georges André Nicolas Citroën né en 1955, ancien élève de l'ENA, directeur de la Stratégie de la SNCF 1999-2002 puis directeur général de Systra, filiale de la RATP et de la SNCF 2002-2010, père de :
Charles-André Citroën
Laeticia Citroën
Gaspard Citroën
Bernard Louis Citroën
Maxime Citroën 1919-1990, époux de Antoinette David-Weill 1920-1980, fille de David David-Weill), père de quatre enfants :
André Citroën
Louis-André Citroën
Jean Citroën, époux d’Élisabeth Lentschner, père de trois filles :
Zelda Citroën
Flora Citroën
Edmée Citroën
René Citroën
Claire Citroën, épouse de Jean-Marc Pequignot, dont postérité :
Antoine Pequignot
Marthe Pequignot
Solange 1924-1925. 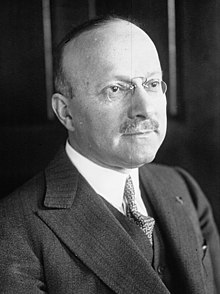 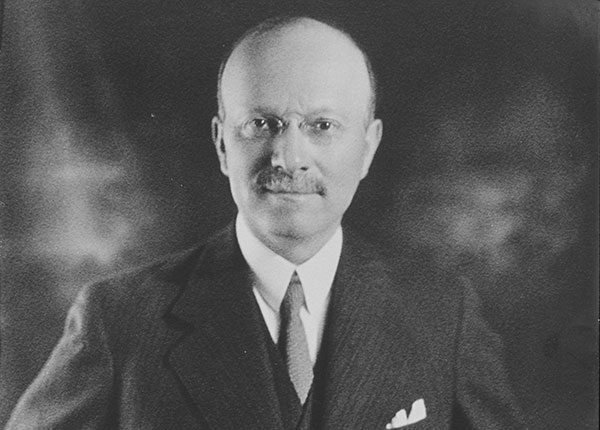    
Posté le : 02/07/2016 23:55
Edité par Loriane sur 05-07-2016 21:42:42
|
|
|
|
|
Blaise Pascal 1 |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
Le 19 juin 1623 naît Blaise Pascal
à Clairmont aujourd'hui Clermont-Ferrand, en Auvergne, mort le 19 août 1662 à 39 ans à Paris, mathématicien, physicien, inventeur, philosophe, moraliste et théologien français de l'école, tradition jansénisme, fidéisme. Ses principaux intérêtssont la philosophie, mathématiques, physique, morale et théologie et ses idées les plus remarquables sont le pari de Pascal, divertissement et misère de la condition humaine, théorème de Pascal, triangle de Pascal, probabilité en mathématiques. Il a été influencé par saint Augustin, Épictète, Montaigne, Jansenius. Il a influencé Arnauld, Nicole, Ravaisson, Lachelier, Duhem, Brunschvicg, van Fraassen, Cioran, Bourdieu, G. K. Chesterton. Les adjectifs dérivés sont pascalien, pascalienne. Sa mère est Antoinette Begon, son père est Étienne Pascal, sa sœur Jacqueline Pascal. Enfant précoce, son père l'éduque. Les premiers travaux de Pascal concernent les sciences naturelles et appliquées. Il contribue de manière importante à l’étude des fluides. Il a clarifié les concepts de pression et de vide, en étendant le travail de Torricelli. Pascal a écrit des textes importants sur la méthode scientifique. À 19 ans, il invente la première machine à calculer et après trois ans de développement et 50 prototypes, il la présente à ses contemporains en la dédiant au chancelier Séguier. Dénommée machine d’arithmétique, puis roue pascaline et enfin pascaline, il en construisit une vingtaine d'exemplaires dans la décennie suivante. Mathématicien de premier ordre, il crée deux nouveaux champs de recherche majeurs : tout d’abord il publie un traité de géométrie projective à seize ans ; ensuite il développe en 1654 une méthode de résolution du problème des partis qui, donnant naissance au cours du XVIIIe siècle au calcul des probabilités, influencera fortement les théories économiques modernes et les sciences sociales. Après une expérience mystique qu'il éprouva à la suite d'un accident de carrosse en octobre 1654, il se consacre à la réflexion philosophique et religieuse. Il écrit pendant cette période Les Provinciales et les Pensées, ces dernières n’étant publiées qu’après sa mort qui survient deux mois après son 39e anniversaire, alors qu’il a été longtemps malade sujet à des migraines violentes en particulier.
En bref
On a tant imaginé et si passionnément considéré Pascal, dit Valéry, qu'on en a fait un personnage de tragédie, une sorte de héros de la dépréciation totale et amère , de Hamlet français et janséniste . Les travaux des historiens modernes achèvent à peine aujourd'hui de corriger cette légende, née des polémiques religieuses des XVIIIe et XIXe siècles.
Le génie de Pascal se caractérise par le refus de la spécialisation qui convient à l'honnête homme. Si Port-Royal le considère comme un maître en véritable rhétorique , et la postérité comme l'un des fondateurs de la prose classique en France, son activité ne se limite pas aux lettres : remarquable géomètre et physicien, il est aussi philosophe, moraliste et théologien. Dans tous les domaines qu'il a abordés, il a su inventer et créer ; mais il s'est surtout montré capable d'établir entre eux des liens qui font de son œuvre l'une des plus puissantes synthèses de la pensée classique.
Outre cela, Pascal est homme d'action concrète. L'invention de la machine arithmétique et des carrosses à cinq sols témoigne de son esprit d'entreprise. Les Provinciales et les Pensées sont, chacun à sa manière, des ouvrages de circonstance, mais l'engagement y est guidé par un souci de la vérité essentielle qui dépasse les bornes des querelles religieuses du temps. Cependant, ce sont surtout son expérience religieuse et la réflexion morale des Pensées qui ont donné à Pascal sa place dans les grands débats philosophiques et spirituels ainsi que dans le développement des lettres en France. Dominique Descotes
Aux confins de la connaissance et de la foi Une formation humaniste.
Blaise Pascal naît le 19 juin 1623 à Clermont en Auvergne, d'Étienne Pascal, président à la Cour des aides, et d'Antoinette Begon (morte en 1626). Son père, fort savant en mathématiques, mécanique et musique, quitte en 1631 sa charge à Clermont pour s'installer, avec son fils et ses deux filles Gilberte et Jacqueline, à Paris où il entre en contact avec le monde scientifique et se lie avec Roberval, le père Mersenne, Girard Desargues entre autres. Il s'occupe seul de l'éducation de Blaise, suivant des principes inspirés par l'humanisme : il attend pour enseigner une matière que l'enfant soit en mesure de la dominer ; il le forme d'abord aux lettres, laissant pour plus tard les sciences mathématiques, mais développe l'esprit de synthèse en exposant d'abord les lois universelles de la grammaire pour montrer ensuite comment elles se diversifient dans les langues particulières. Cette pédagogie éveille si bien l'esprit du jeune Blaise qu'il parvient à redécouvrir seul certaines propositions d'Euclide avant d'avoir été initié à la géométrie. Cette formation comporte un aspect philosophique et religieux, notamment dans la règle de séparation des sciences et de la religion : « Tout ce qui est l'objet de la foi ne saurait l'être de la raison, et beaucoup moins y être soumis. » Malgré sa jeunesse, Blaise participe activement aux séances où les membres de l'académie Mersenne soumettent leurs travaux à l'examen de leurs pairs. Il s'y imprègne de l'esprit scientifique « mécaniste » qui s'oppose à l'aristotélisme des facultés, ainsi qu'au cartésianisme, souvent considéré comme une sorte de scolastique moderne. L'écho de cette formation est encore sensible dans les Pensées.
En 1639, Étienne Pascal reçoit de Richelieu une mission de commissaire à la levée des impôts en Normandie, charge qui l'intègre au corps plein d'avenir des officiers attachés au service direct du roi. L'attachement des Pascal à la couronne restera constant ; quelques années plus tard, lors de la Fronde, Blaise se singularisera dans le milieu de Port-Royal par son loyalisme déclaré et son hostilité envers toute rébellion. La vive critique du manque de justice effective des lois humaines qu'on trouve dans les Pensées (fragment Lafuma 60, Sellier 94) ne contredit pas ce loyalisme : si Pascal admet que l'ordre politique est fondé sur la force, plutôt que sur une justice effective que l'homme ne connaît que par les lois de Dieu, il n'en juge pas moins dangereux de le remettre en cause, car la révolte engendre la guerre civile sans jamais établir une société meilleure ; le respect de l'ordre dont Dieu a permis l'établissement, sous réserve qu'il ne soit pas tyrannique, demeure donc le seul parti raisonnable.
Les expériences scientifiques. Les Pascal résident à Rouen de 1640 à 1647. Blaise poursuit une intense activité scientifique (recherches sur le vide, invention de la machine arithmétique). Dès ces premiers travaux éclate son aptitude à saisir dans ce qu'ils ont de concret les problèmes significatifs et les méthodes fécondes. En géométrie, malgré le style bizarre du Brouillon project d'une atteinte aux événements des rencontres du cône avec un plan (1639), il reconnaît en Desargues l'inventeur d'une méthode originale qui permet, par la considération purement géométrique des sections coniques par « projection optique », d'établir une théorie générale des courbes du second degré. De la même manière, Pascal saisit immédiatement l'intérêt de l'expérience du vide réalisée par Torricelli : à partir de cette première invention, il en réalise une multitude d'autres, avec des soufflets, des seringues, des siphons et des tubes parfois longs de 12 mètres ; cette variété d'instruments lui permet d'approcher le phénomène du vide sous tous ses aspects. Un souci comparable de décrire un phénomène dans ses manifestations les plus différentes inspirera les fragments des Pensées sur le « divertissement », que Pascal présente dans une multitude de conduites sociales : chasse, jeu, danse, carrière politique, etc. Il fait de Pascal un précurseur de l'esprit expérimental moderne. Ce sens aigu du concret paraît aussi chez l'homme d'action. Avec l'invention de la machine arithmétique, en 1645, Pascal emploie sa science mathématique au soulagement de l'effort de calcul auquel sa charge contraint son père. Mais il sait adapter l'appareil à différents usages pratiques : calcul abstrait, calcul financier, calcul des longueurs pour le toisé des architectes ; plusieurs dispositifs ingénieux contribuent à en multiplier les usages et les possibilités techniques. Les compétences de Pascal en hydrostatique sont aussi mises à profit dans l'entreprise d'assèchement des marais poitevins, dont il est sociétaire et conseiller scientifique. On ne s'étonne donc pas de le voir, vers la fin de sa vie, fonder avec le duc de Roannez l'entreprise des carrosses à cinq sols, première forme des transports collectifs urbains, qui comporte un réseau de lignes à travers Paris, avec stations et changements. Le soin d'assurer la sécurité intérieure et extérieure des véhicules, les mesures prises pour faciliter leur usage aux handicapés et le prix relativement modique du transport expliquent le succès de l'opération. Pascal sait d'ailleurs gérer ses entreprises en les développant par la création de lignes nouvelles et en les protégeant par des privilèges.
Le sens du concret n'exclut pas la recherche constante de l'universalité. En physique, une fois le fait du vide rigoureusement prouvé, Pascal passe rapidement à la recherche de la « raison des effets », de la loi abstraite qui commande la diversité des phénomènes : en 1648, il demande donc à son beau-frère d'effectuer sur le puy de Dôme l'expérience cruciale qui doit confirmer la réalité de la pression atmosphérique et la théorie générale de l'équilibre des liqueurs dont le vide n'est qu'une conséquence. La réflexion philosophique suit une voie semblable : Pascal ne s'arrête guère au fait que la preuve du vide ruine la physique scolastique ; en revanche, le jésuite Étienne Noël ayant contesté ses expériences, il saisit l'occasion pour construire une théorie d'ensemble de la méthode expérimentale. Quelques années plus tard, L'Équilibre des liqueurs et La Pesanteur de la masse de l'air s'achèvent aussi par une ample Conclusion sur les voies du progrès de l'esprit humain dans la recherche de la vérité. Vers la même époque, les traités relatifs au triangle arithmétique trouvent leur prolongement dans L'Esprit géométrique (1655 selon J. Mesnard), brillante mise au point épistémologique sur les règles des définitions, des axiomes et des démonstrations. Enfin, dans l'œuvre religieuse, après avoir publié dix Provinciales, Pascal propose dans la onzième une justification du style plaisant qui a fait leur succès, fondée sur une théorie rhétorique générale de la polémique chrétienne. Ce mouvement qui, du singulier, va aux fondements universels, se retrouve partout dans son œuvre.
Un art de la persuasion. Dans ses activités, Pascal est servi par un grand sens de la communication : plus que tout autre en son temps, il a saisi les exigences du contact entre les esprits et de l'« art de persuader », pour reprendre le titre donné à la seconde section de L'Esprit géométrique. Marc Fumaroli a montré qu'il s'inscrit dans la tradition rhétorique humaniste des milieux parlementaires et gallicans, par son idéal d'une éloquence haute et toujours fondée en vérité. Il est marqué aussi par la rhétorique chrétienne dont il trouve des modèles chez saint Augustin et, parmi les modernes, chez Saint-Cyran. Mais Pascal a aussi pour maître d'honnêteté Montaigne ; il a fréquenté le monde, dont les exigences de clarté, d'aisance, d'agrément et le dégoût de la rhétorique scolaire l'ont profondément impressionné. Dans son œuvre tant scientifique que littéraire paraît toujours le souci de concilier les grandes vérités de la raison et de la foi avec une expression accessible à tous : le succès sans précédent des Provinciales tient essentiellement à son art d'y mettre les problèmes de théologie à la portée des gens du monde, y compris, disait-on, des femmes dont l'éducation ne comportait pas l'étude du latin. Cet idéal rhétorique répond à l'idéal moral de l'honnête homme : le style naturel, contraire à la fois au bouffon et à l'enflé, donne au lecteur l'agréable surprise de rencontrer, au lieu d'un auteur infatué de ses livres, un homme qui sait répondre aux besoins d'autrui. Les Provinciales (1656-1657) témoignent de l'aisance avec laquelle, selon les circonstances, le sujet et les dispositions de leurs destinataires, Pascal passe de l'ironie et de la raillerie plaisante des premières lettres contre les casuistes à la haute éloquence des dernières, toujours pour la défense de la morale chrétienne et des innocents persécutés. Entre la satire corrosive de la vanité humaine et les visions cosmiques de « Disproportion de l'homme », les Pensées jouent sur une pareille variété de registres. Pour toucher son lecteur, Pascal sait aussi mettre en œuvre des techniques audacieuses, qui annoncent la publicité moderne. Pour la machine arithmétique, il rédige un Avis nécessaire, sorte de prospectus qui en vante les qualités : éloge de sa beauté, de sa commodité, de son « ergonomie » et d'une solidité éprouvée par des tests ; il en fait démontrer le fonctionnement aux acheteurs virtuels par Roberval, et va lui-même la présenter dans le monde. Le savant fait preuve du même sens publicitaire : en 1648, le Récit de la grande expérience de l'équilibre des liqueurs (l'expérience du puy de Dôme) conte en termes pittoresques, très différents des traités de physique contemporains, le déroulement d'une entreprise à laquelle Pascal veut donner un retentissement inhabituel, en raison de son caractère décisif.
Tous ces traits ne concordent guère avec l'image d'intellectuel de cabinet qui est souvent celle de Pascal, et il faut en rabattre aussi sur celle du malade éternellement en proie à des angoisses morbides, voire à des visions, que les philosophes du XVIIIe siècle ont accréditée à des fins de propagande. S'il est vrai que Pascal a souvent été en proie à des crises de coliques, à des migraines ou à des paralysies partielles qui lui ont interdit toute activité à certaines périodes de sa vie, il n'a jamais été un malade perpétuel, et en tout état de cause, comme l'écrit Jean Mesnard, son génie « ne s'explique pas par la maladie, au contraire, s'il a pu s'épanouir, c'est malgré la maladie ».
Port-Royal. C'est en 1646, à Rouen, que Pascal rencontre l'augustinisme grâce aux frères Deschamps, deux médecins venus soigner son père, qui lui font lire des ouvrages de Saint-Cyran et peut-être de Jansénius, dont il est si fortement frappé que, dans cette famille dont le catholicisme a été jusqu'alors tiède, il engendre un mouvement de ferveur qui touche particulièrement sa sœur Jacqueline. Cette première conversion ne le conduit pas de l'incroyance à la foi : c'est le premier pas d'un progrès qui mène d'une foi médiocre à une piété ardente. La vie de Pascal peut être considérée comme une conversion continuée, qui comporte aussi ses temps de stagnation et ses reculs. Lorsqu'en 1647 Pascal convalescent regagne Paris avec Jacqueline, ses contacts avec Port-Royal deviennent fréquents. Mais, après la mort de son père et l'entrée de sa sœur en religion, commence la « période mondaine » durant laquelle il cherche sa voie du côté des sciences et de la vie de société. Quelques années suffisent cependant pour qu'une grande sécheresse spirituelle le saisisse : il confie à Jacqueline qu'au milieu « de ses occupations [...] et parmi toutes les choses qui pouvaient contribuer à lui faire aimer le monde [...], il était de telle sorte sollicité de quitter tout cela, et par une aversion extrême qu'il avait des folies et des amusements du monde, et par le reproche continuel que lui faisait sa conscience, qu'il se trouvait détaché de toutes choses [...], mais que d'ailleurs il était dans un si grand abandonnement du côté de Dieu, qu'il ne sentait aucun attrait de ce côté-là ». La crise se dénoue dans la nuit du 23 novembre 1654, par une expérience mystique du « Dieu sensible au cœur » dont Pascal garde le souvenir dans le Mémorial cousu dans la doublure de son vêtement. Dès lors, Pascal se lie très étroitement au groupe de Port-Royal, où il tient une place importante. Contrairement à une légende malveillante, il n'y fait nullement figure d'ignorant : les travaux de Philippe Sellier ont révélé la connaissance approfondie de la pensée de saint Augustin dont témoignent ses écrits. La solidité de sa doctrine théologique paraît dans la récente édition des Écrits sur la grâce due à Jean Mesnard (selon qui ils furent rédigés entre l'automne de 1655 et le printemps de 1656), et qui constituent l'une des plus claires synthèses sur les problèmes fondamentaux de la prédestination. Pour Pascal, la vérité chrétienne tient le milieu entre les erreurs contraires du calvinisme et du pélagianisme. À l'origine, Dieu veut sauver tous les hommes, et accorde à Adam la grâce nécessaire pour faire à volonté le bien ou le mal ; librement commis par l'homme, le péché originel blesse gravement sa nature, détournant son cœur de Dieu pour le soumettre à la concupiscence, désir de tout pour soi qui engendre en l'homme une délectation dans le mal à laquelle il cède infailliblement. Par une miséricorde gratuite, Dieu choisit, dans la masse digne de perdition, des personnes auxquelles il accorde une grâce qui fait naître dans le cœur une délectation dans le bien qui rompt les chaînes de la concupiscence, et leur permet d'accomplir librement ses commandements. Pour Pascal, comme pour Saint-Cyran, la conversion engendre un renouvellement profond de l'âme, entièrement tournée vers le Dieu de Jésus-Christ : elle s'accommode mal d'une foi tiède. On comprend ainsi la passion avec laquelle Pascal s'engage dans la campagne des Provinciales : à l'origine de ces dix-huit lettres se trouve la nécessité de défendre Antoine Arnauld et Port-Royal contre la persécution par les autorités politiques et ecclésiastiques. Mais, bientôt, Pascal se tourne contre la morale laxiste des casuistes, dont les Jésuites sont alors les principaux défenseurs. Ce qui le scandalise, ce sont moins les opinions probables, souvent ridicules, parfois révoltantes, de leurs docteurs (autorisation du vol, du duel, de l'assassinat, marchandage sur l'amour de Dieu) que la manière dont ils substituent la satisfaction de l'amour propre à la recherche sincère du sûr par amour de Dieu, nerf de la vie chrétienne. Outre le public mondain, les Provinciales touchent les magistrats et les curés des paroisses, fort attachés aux libertés gallicanes et hostiles à la Compagnie de Jésus, réputée agent de l'impérialisme romain. Lorsque le jésuite Pirot eut la maladresse de justifier dans une Apologie pour les casuistes les maximes laxistes incriminées dans les Provinciales, les curés de France parvinrent, par une campagne d'écrits dont plusieurs sont de Pascal, à obtenir des censures ecclésiastiques.
Pascal est pourtant contraint de revenir à la défense des religieuses et des messieurs de Port-Royal contre les reproches d'hérésie qui les accablent. Lorsque les autorités ecclésiastiques exigent de tous les religieux la signature d'un formulaire condamnant Jansénius, il défend une attitude de netteté sans rébellion, et ce n'est qu'en 1661, lorsqu'il constate son désaccord sur la tactique avec ses amis de Port-Royal, qu'il se retire des polémiques.
Le projet d'Apologie. Il se consacre alors complètement à son projet d'Apologie de la religion chrétienne, dont certaines idées remontent aux discussions qu'il a eues en 1655 avec Lemaître de Sacy, et qui s'enracine dans une réflexion sur les miracles inspirée par la guérison de sa nièce Marguerite Périer par l'attouchement de la Sainte Épine. Comme l'édition des Pensées procurée par Port-Royal en 1670 à partir des papiers posthumes de Pascal ne donne qu'une idée très déformée de l'original, la genèse de son ouvrage nous serait inconnue si Gilberte n'avait conservé et fait copier les manuscrits. Mais ce n'est qu'au XIXe siècle que la découverte du manuscrit original par Victor Cousin a permis aux éditeurs de chercher à restituer fidèlement le travail de Pascal. Après de nombreuses éditions arbitraires, celles de Louis Lafuma et de Philippe Sellier fournissent un texte fidèle. Plusieurs érudits ont étudié de très près les papiers laissés par Pascal. Yoichi Maeda a mis au point une méthode de lecture qui suit, selon l'ordre génétique, les différents états des fragments des Pensées, avec leurs corrections et leurs ratures, et permet de mesurer de façon rigoureuse les bouleversements parfois profonds imposés par l'auteur à ses premières rédactions. De son côté, Pol Ernst aborde le manuscrit par ses aspects les plus matériels : partant du fait que Pascal écrivait sur de grandes feuilles qui furent ensuite découpées par lui-même d'abord pour en répartir les morceaux dans divers dossiers de travail, par d'autres ensuite dans un but de conservation, il examine la texture du papier, les filigranes, les pontuseaux, la manière dont les fragments ont été découpés ; il parvient ainsi à reconstituer en totalité ou en partie un nombre considérable de feuillets originaux tels qu'ils étaient avant le découpage, qui donnent à voir le jaillissement même de la pensée pascalienne. Pol Ernst arrive aussi à dater certaines rames de papier employées par Pascal, dont la succession reflète la genèse de l'ensemble de l'ouvrage. L'édition établie par Philippe Sellier en 1976 à partir de la copie de l'original réalisée sous la direction de Gilberte Périer va dans le même sens : à côté des vingt-huit dossiers dotés d'un titre qui forment l'armature du projet apologétique, l'éditeur distingue plusieurs groupes de dossiers, tous constitués par Pascal à des fins diverses, les uns destinés à recueillir les « chutes » et les fragments rejetés, d'autres servant de réservoirs de « pensées mêlées » en attente d'emploi, d'autres enfin réunissant des textes en cours de travail, soit que Pascal étende et améliore des rédactions antérieures, soit qu'il assemble des notes en vue de développements complémentaires. Toutes ces recherches révèlent un écrivain très éloigné du génie exalté imaginé par les romantiques, fort maître de ses techniques de composition et chez qui le mouvement créateur n'exclut jamais l'emploi d'une méthode rigoureuse.
Dans son projet apologétique, Pascal ne prétend évidemment pas communiquer à son lecteur une foi qui ne peut être donnée que par Dieu ; il croit aussi inutile de prouver l'existence de Dieu par les sciences ou les arguments métaphysiques, qui conduisent plutôt au déisme qu'à la religion du Christ. Son principal objectif est de vaincre l'indifférence des incroyants qui, comme le Dom Juan de Molière, ont perdu le souci de leur propre destin ; il croit aussi possible d'éliminer les philosophies fallacieuses par lesquelles l'homme se dissimule son ignorance, et d'orienter la recherche dans le bon sens. Son projet comporte donc un premier volet réfutatif, fondé sur l'étude morale de l'homme. Pascal adopte d'abord le point de vue sceptique de Montaigne pour montrer la vanité et la misère humaines : incapacité de connaître le vrai et le bien, d'instituer des lois justes, domination par les puissances trompeuses, inconstance dans les idées, la morale et la vie sociale, autant de thèmes empruntés aux Essais. Après avoir ainsi confondu sa présomption, il montre que la conscience de sa propre misère atteste en l'homme une certaine grandeur, qu'ont exaltée des philosophes comme Descartes, le « docteur de la raison » et le stoïcien Épictète. Ce mélange de grandeur et de bassesse ferait de l'homme un être incompréhensible, si Pascal ne dépassait les limites de la philosophie naturelle pour faire appel à un principe d'origine surnaturelle, la doctrine du péché originel, qui, tout incompréhensible qu'elle soit, n'en explique pas moins la contrariété de la nature humaine, en rapportant ses aspects de grandeur à un vestige de l'innocence d'avant la Chute, et sa misère à la corruption qui suit le péché originel.
Reste à confirmer cette hypothèse dans une seconde partie d'ordre historique. Examinant si Dieu a donné des marques de la véritable religion, Pascal oriente l'attention sur le peuple juif et l'annonce messianique des prophètes d'Israël. Sa preuve « des deux Testaments à la fois » consiste à montrer que « les prophéties de l'un sont accomplies en l'autre ». Concédant que, si ces prophéties n'ont qu'un sens littéral, elles peuvent être rangées au magasin des illusions, il argue qu'en revanche, si elles ont un sens figuré et spirituel, on peut montrer que le Messie est venu en Jésus-Christ. Une solide théorie de l'interprétation permet à Pascal de prouver que le Christ remplit toutes les conditions requises par les prophètes.
Le célèbre argument du « pari » aurait sans doute pris place à la charnière de cette Apologie, au terme de la démonstration anthropologique, pour encourager le lecteur à poursuivre la recherche dans l'Écriture et l'histoire sainte. Il ne s'agit pas d'une preuve de l'existence de Dieu : l'argument part au contraire de l'hypothèse qu'on ne peut établir ni que Dieu est, ni qu'il n'est pas. De quoi Pascal tire que, dans le doute, la suspension de jugement dans laquelle se réfugie l'incrédule indifférent est une conduite à la fois contraire aux principes du bon sens et suicidaire ; s'il pouvait croire, sa conversion serait raisonnable. Naturellement, cette argumentation se heurte au fait que nul ne peut acquérir la foi à volonté, puisqu'elle est un don de la grâce divine. Pascal en est bien conscient : dans son esprit, le pari ne s'identifie nullement avec l'acte de foi ; il consiste seulement à comprendre que la recherche est nécessaire, et qu'elle doit commencer par la suppression des obstacles, c'est-à-dire la modération des passions qui s'opposent à l'action de la grâce en l'homme. La conclusion de l'Apologie aurait repris la même idée avec plus d'ampleur, puisque, au terme de sa démonstration historique, Pascal conclut qu'il « y a loin de la connaissance de Dieu à l'aimer », c'est-à-dire à la conversion. Un engagement personnel est indispensable pour trouver le Dieu sensible au cœur. Pascal meurt sans avoir achevé son ouvrage, au terme d'une vie qui a donné à ses proches l'impression de la sainteté.
Les études pascaliennes ont pris un tour nouveau sous l'impulsion de la grande édition des Œuvres complètes par Jean Mesnard, qui a révélé plusieurs inédits et rendu la place qui leur était due à des textes jusqu'alors méconnus en raison d'une présentation défectueuse. Les Écrits sur la grâce, édités depuis toujours sans ordre logique ni chronologique, revêtent aujourd'hui la forme d'un ensemble de trois pièces complètes, classées selon leur succession génétique. En outre, la recherche met encore au jour des textes nouveaux : en 1994, Pascale Mengotti a retrouvé, à la bibliothèque de l'Institut de France, un manuscrit original autographe des Mémoires de Nicolas Fontaine, qui a permis la publication, avec Jean Mesnard, d'une version de l'Entretien avec M. de Sacy notablement améliorée, qui rend caduques toutes les précédentes, fondées sur des sources défectueuses. L'étude de ce texte nouveau a permis à Jean Mesnard d'établir qu'il se fonde sur un « rapport » original de Pascal concernant ses lectures philosophiques, suivi de très près par le rédacteur. Seule la découverte du manuscrit primitif permettrait d'améliorer encore le texte. Cet exemple fait espérer que seront un jour redécouverts des ouvrages complètement disparus, mais dont l'intérêt a été reconnu par ceux qui les ont consultés, comme le Traité des coniques 1640 dont ne subsistent que les premières pages. On peut attendre dans l'avenir un enrichissement substantiel de la connaissance de Pascal, l'homme et l'écrivain. Dominique Descotes
Sa vie
Né à Clairmont aujourd'hui Clermont-Ferrand, en Auvergne, Blaise Pascal perd sa mère, Antoinette Begon, à l’âge de trois ans.
Son père, Étienne Pascal 1588-1651 très intéressé par les mathématiques et les sciences, était conseiller du roi pour l'élection de Basse Auvergne, puis second président à la Cour des aides de Montferrand, et décide d'éduquer seul ses enfants. Blaise Pascal avait deux sœurs, Jacqueline, née en 1625, et Gilberte née en 1620, mariée en 1642 à Florin Périer qui lui survécut.
En 1631, Étienne se rend avec ses enfants à Paris, alors que Blaise n'a encore que 8 ans. Il décide d’éduquer lui-même son fils qui montrait des dispositions mentales et intellectuelles extraordinaires. En effet très tôt, Blaise a une capacité immédiate pour les mathématiques et la science, peut-être inspiré par les conversations fréquentes de son père avec les principaux savants de l’époque : Roberval, Mersenne, Desargues, Mydorge, Gassendi et Descartes.
À onze ans, il compose un court Traité des sons des corps vibrants et aurait démontré la 32e proposition du Ier livre d’Euclide concernant la somme des angles d'un triangle. Étienne réagit en interdisant à son fils toute poursuite de ses études en mathématiques jusqu’à quinze ans, afin qu’il puisse étudier le latin et le grec. Sainte-Beuve dans son Port-Royal, III, p. 484 raconte : Je n’ai rien à dire des éléments de géométrie, si ce n’est que Pascal, qui les avait lus en manuscrit, les jugea si clairs et si bien ordonnés, qu’il jeta au feu, dit-on, un essai d’éléments qu’il avait fait lui-même d’après Euclide, et qu’Arnauld avait jugé confus ; c’est même ce qui avait d’abord donné à Arnauld l’idée de composer son essai : en riant, Pascal le défia de faire mieux, et le docteur, à son premier loisir, tint et gagna la gageure.
À douze ans 1635, il commence à travailler seul sur la géométrie. Le travail de Desargues l'intéressa particulièrement et lui inspira, à seize ans, un traité sur les sections coniques : Essai sur les coniques. La majeure partie en est perdue mais un résultat essentiel et original en reste sous le nom de théorème de Pascal. Le travail de Pascal était si précoce que Descartes, en voyant le manuscrit, crut qu’il était de son père.
En 1638, Étienne, opposé aux dispositions fiscales du cardinal de Richelieu, quitte Paris avec sa famille pour échapper à la Bastille. Lorsque Jacqueline, sœur de Blaise, dit un compliment particulièrement bien tourné devant Richelieu, Étienne obtient sa grâce. En 1639, la famille s’installe à Rouen où Étienne devient commissaire délégué par le Roi pour l’impôt et la levée des tailles.
À dix-huit ans 1641, Pascal commence le développement de la Pascaline, machine à calculer capable d’effectuer des additions et des soustractions afin d’aider son père dans son travail. Il en écrit le mode d’emploi : Avis nécessaire à ceux qui auront la curiosité de voir ladite machine et s’en servir. Plusieurs exemplaires sont conservés, en France, au Musée des arts et métiers à Paris et au musée de Clermont-Ferrand. Bien que ce soit le tout début du calcul mécanique, ce fut un échec commercial à cause de son coût élevé 100 livres. Pascal améliorera la conception de la machine pendant encore dix années et en construira une vingtaine d’exemplaires.
Pascaline.
Pascal est également à l’origine de l’invention de la presse hydraulique, s'appuyant sur le principe qui porte son nom.
On lui attribue également l’invention de la brouette ou vinaigrette, et du haquet, véhicule hippomobile conçu pour le transport des marchandises en tonneaux. Ces attributions semblent remonter à un ouvrage de Bossut, qui réalise la première édition complète des écrits de Pascal, dans l’avertissement duquel il mentionne ces inventions d’après le témoignage de M. Le Roi, de l’Académie des Sciences, qui tient ses informations de son père, Julien Le Roi11.
Derniers travaux et décès
Épitaphe de Pascal dans l'église Saint-Étienne-du-Mont, 5e arrondissement de Paris
T. S. Eliot décrit Pascal, à cette période de sa vie, comme un homme mondain parmi les ascètes et comme un ascète parmi les hommes du monde . Le style de vie ascétique de Pascal venait de sa foi en ce qu'il était naturel et normal pour un homme de souffrir. Dans ses dernières années troublées par une mauvaise santé, il rejette les ordonnances de ses médecins en disant : La maladie est l'état naturel du chrétien. D'après sa sœur Gilberte, il aurait écrit alors sa Prière pour demander à Dieu le bon usage des maladies.
En 1659, Pascal tombe sérieusement malade.
Louis XIV a interdit le mouvement janséniste de Port-Royal en 1661. En réponse, Pascal a écrit un de ses derniers travaux, Écrit sur la signature du formulaire, recommandant instamment aux jansénistes de ne pas le signer. Plus tard au cours de cette année, sa sœur Jacqueline meurt, ce qui convainc Pascal de cesser sa polémique à propos du jansénisme.
Grâce à ses connaissances en hydrostatique, il participe à l’assèchement des marais poitevins, à la demande du Duc de Roannez. C'est avec ce dernier qu'il inaugurera la dernière de ses réalisations qui reflète parfaitement le souci d’action concrète qui habite le savant : la première ligne de transports en commun, convoyant les passagers dans Paris avec des carrosses à cinq sols munis de plusieurs sièges.
Testament de Blaise Pascal, Archives nationales de France.
En 1662, la maladie de Pascal est devenue plus violente. Conscient du fait qu'il a peu de chances de survivre, il songe à trouver un hôpital pour les maladies incurables, mais ses médecins le déclarent intransportable. À Paris, le 17 août 1662, Pascal a des convulsions et reçoit l’extrême onction. Il meurt le matin du 19 au no 8 de la rue Neuve-Saint-Étienne-du-Mont devenue le no 2 de la rue Rollin, ses derniers mots étant Puisse Dieu ne jamais m'abandonner. Il est enterré dans l'église Saint-Étienne-du-Mont.
L'autopsie pratiquée après sa mort révélera de graves problèmes stomacaux et abdominaux, accompagnés de lésions cérébrales. Malgré cette autopsie, la raison exacte de sa santé chancelante n'est pas connue.
Des spéculations ont eu lieu à propos de tuberculose, d'un cancer de l'estomac ou d'une combinaison des deux. Les maux de tête qui affectaient Pascal sont attribués à la lésion cérébrale. Marguerite Périer, sa nièce, dit dans sa biographie de Pascal que l'autopsie révéla que le crâne ne comportait aucune trace de suture autre que la lambdoïde… avec une abondance de cervelle, dont la substance était si solide et si condensée….
Les professeurs M. Dordain et R. Dailly de la Faculté de Médecine de Rouen développent, dans les années 1970, les travaux de MM. Augeix, Chedecal, Crussaire et Nautiacq et établissent un diagnostic d’insuffisance rénale chronique avec suspicion d’une maladie polykistique des reins et présence de lésions vasculaires cérébrales en voie de complications thrombose. Pascal aurait donc été atteint d’une maladie génétique… dont les expressions cliniques entrent dans le cadre des dystrophies angioplasiques congénitales… objet de travaux Pr J.-M. Cormier et Dr J.-M. André, 1978 et 1987 ces dernières années.
Miracle
Quand Pascal revient à Paris, juste après avoir surveillé la publication de sa dernière lettre, sa croyance religieuse est renforcée par sa proximité avec un miracle apparent qui concerne sa nièce Marguerite Périer âgée de dix ans, dans la chapelle du couvent de Port-Royal. Sa sœur Gilberte Périer raconte dans La vie de Monsieur Pascal qu’elle a consacrée à son frère :
Ce fut en ce temps-là qu’il plut à Dieu de guérir ma fille d’une fistule lacrymale, dont elle était affligée il y avait trois ans et demi. Cette fistule était d’une si mauvaise qualité, que les plus habiles chirurgiens de Paris la jugèrent incurable. Et enfin Dieu s’était réservé de la guérir par l’attouchement d’une Sainte-Épine qui est à Port-Royal des Champs ; et ce miracle fut attesté par plusieurs chirurgiens et médecins, et autorisé par le jugement solennel de l’Église.
Plus tard, les jansénistes et les catholiques utilisèrent pour leur défense ce miracle bien documenté. En 1728, le pape Benoît XIII s’en servit pour montrer que l’âge des miracles n’était pas terminé.
Pascal mit dans son blason un œil surmonté d’une couronne d’épines, avec l’inscription Scio cui credidi Je sais en qui j'ai cru. Sa foi renouvelée, il se décida à écrire son œuvre testamentaire, inachevée, les Pensées.
Pensées
Pascal ne put achever, avant de mourir, son travail théologique le plus important : un examen soutenu et logique de la défense de la foi chrétienne, avec pour titre original Apologie de la religion chrétienne.
Après sa mort, de nombreuses feuilles de papier ont été trouvées lors du tri de ses effets personnels, sur lesquelles étaient notées des pensées isolées, feuilles regroupées en liasses dans un ordre provisoire mais parlant. La première version de ces notes éparses est imprimée en 1669 sous le titre Pensées de M. Pascal sur la religion et sur quelques autres sujets. Elles sont devenues très vite un classique. Parce que ses amis et les disciples de Port-Royal étaient conscients que ces pensées » fragmentaires pouvaient mener au scepticisme plutôt qu’à la piété, ils ont caché les pensées sceptiques et ont modifié une partie du reste, de peur que le roi ou l’église n’en prenne offense alors que la persécution de Port-Royal avait cessé, et les rédacteurs ne souhaitaient pas une reprise de la polémique. Il a fallu attendre le xixe siècle pour que les Pensées soient publiées complètement et avec le texte d’origine, tirées de l'oubli et éditées par le philosophe Victor Cousin.
Les Pensées de Pascal sont largement considérées comme une des pièces maîtresses et une étape de la littérature française. En présentant ses observations sur un chapitre, Sainte-Beuve considérait ces pages comme les plus fines de la langue française. Will Durant, dans son onzième volume de l’Histoire des civilisations, le juge comme le livre le plus éloquent en français. Dans les Pensées, Pascal présente plusieurs paradoxes philosophiques : infini et néant, foi et raison, âme et matière, mort et vie, sens et vanité – apparemment n’arrivant à aucune conclusion définitive sans l’appui de l’humilité et de la grâce. En les rassemblant, il développe le pari de Pascal.
Vie religieuse
Cornelius Jansen
D’un point de vue biographique, deux influences de base le guident vers sa conversion : le jansénisme et la maladie.
Les enfants Pascal ont reçu une éducation chrétienne de la part de leur père et de leur gouvernante Louise Delfault. On peut s’en rendre compte en lisant les poèmes de Jacqueline. Étienne reçoit les plus grands esprits. Certains se vantent d’être libertins, d’avoir secoué le joug de la religion. Étienne les écoute et les réfute avec une telle force de conviction que Blaise en est frappé et rêve de devenir un jour non seulement mathématicien, mais défenseur de la religion. De plus Étienne laisse à son fils cette consigne : « tout ce qui est l’objet de la foi ne le saurait être de la raison ». En 1645, d’après deux textes de Jacqueline et trois de Pascal, Pascal semble avoir eu une déception amoureuse qui faillit lui être fatale. Il décide de ne pas se marier.
En 1646, le père de Pascal s’est démis la cuisse en tombant sur la glace, il est soigné par deux médecins jansénistes (ces frères Deschamps ayant été anoblis sous les noms de La Bouteillerie et Des Landes), disciples de Jean Duvergier de Hauranne (abbé de Saint-Cyran) qui introduisit le jansénisme en France13. Blaise parle fréquemment avec eux durant les trois mois du traitement de son père, il leur emprunte des livres d’auteurs jansénistes, enthousiasmé en particulier par le Discours de la réformation de l'homme intérieur écrit par Cornelius Jansen en 1628, dont il ressort si vivement marqué qu'il communique son admiration à ses proches, certains affirmant donc que ce fut là la date de sa « première conversion ». Il est fortement marqué par leur témoignage. Par eux, Dieu l’appelle. Il répond en se donnant à Lui, il communique sa ferveur à ses proches, et Jacqueline jusqu’alors écartelée entre l’amour de Dieu et le monde où elle brille veut devenir religieuse. Ce n’est pas une conversion ; selon le mot de Jacqueline c’est un Progrès. (Il faut lire le témoignage de sa sœur Gilberte sur Pascal. Il n’est question ni de jansénisme, ni de Port-Royal, ni de conversion).
Il découvre que marcher sur les traces de Copernic et de Galilée pour libérer la physique du poids mort d’Aristote et de la scolastique n’est que la démarche d’une vaine raison, impliquée dans la souillure de l’humanité tout entière, et que tout ce génie qui bouillonne en lui ne le conduit qu’à le divertir d’une révélation terrible et rédemptrice. Que signifie un savoir qui ne jette pas l’homme au pied de la Croix ? Dans cette période, Pascal vit une sorte de « première conversion » et commence, au cours de cette année, d’écrire sur des sujets théologiques. Toute sa famille se met à « goûter Dieu » avec lui.
Dès sa dix-huitième année, il subit un mal nerveux qui le laisse rarement un jour sans souffrance. En 1647, une attaque de paralysie l’atteint au point qu’il ne peut plus se mouvoir sans béquilles. Il a mal à la tête, des maux de ventre, ses jambes et ses pieds sont continuellement froids et demandent des soins pour activer la circulation sanguine ; il porte des bas trempés dans de l’eau-de-vie pour se réchauffer les pieds. En partie pour avoir de meilleurs traitements médicaux, il se rend à Paris avec sa sœur Jacqueline. Sa santé s’améliore mais son système nerveux est perturbé de manière permanente. Dorénavant, il est sujet à une profonde hypocondrie, qui a affecté son caractère et sa philosophie. Il est devenu irritable, sujet à des accès de colère fière et impérieuse, et il sourit rarement.
Pascal s’éloigne de son premier engagement religieux et il vit pendant quelques années ce qu’il a appelé « une période mondaine » (1648-1654). Ce sont les expériences sur le vide, à la suite des travaux de Torricelli, qui l'occupent pleinement. De 1646 à 1654, il multiplie les expérimentations avec toutes sortes d’instruments. L’une d’entre elles, en 1648, lui permet de confirmer la réalité du vide et de la pression atmosphérique et d’établir la théorie générale de l’équilibre des liquides.
Son père meurt en 1651 et Pascal prend possession de son héritage et de celui de sa sœur Jacqueline. Le 4 janvier 1651, en dépit de l’opposition de son frère, Jacqueline entre à Port-Royal de Paris. Légalement, elle perd ses droits civiques. Pascal se coupe de Port-Royal pendant deux ans et neuf mois, sauf quelques entrevues orageuses avec sa sœur. L’entrée de sa sœur au couvent déclenche chez Pascal une dépression. Les médecins lui conseillent de se marier, de prendre une charge. Pascal s’y oppose, les médecins insistent. Finalement Pascal accepte et fait des démarches dans ce sens. Il aurait pu, marié, garder sa fidélité à Dieu comme les deux infirmiers, comme Monsieur Gaston de Renty dont il a lu la vie écrite par Saint-Jure un jésuite, mais il comprend vite que ce n’est pas sa voie. En septembre 1652, il part à Clermont-Ferrand où Florin vient d’acheter Bienassis avec son beau château. Il y restera huit mois. Bienassis jouxte le domaine des carmes déchaussés où Pascal retrouve Blaise Chardon son cousin et ami d’enfance qui est religieux. Pascal fait une première retraite qu’attestera sa sœur et il lit Jean de la Croix. Il découvre la contemplation et devient mystique. Au moment de prononcer ses vœux en juin 1653, Jacqueline veut faire une dot importante au monastère, ce qui est illégal. En mai, Pascal est à Clermont. Avec Florin Périer, époux de Gilberte, ils refusent en se plaçant sur le plan juridique. Pascal rentre à Paris pour régler l’affaire. Entrevue orageuse ! Finalement il sera généreux.
Ainsi, Pascal se trouve à la fois riche et libre. Il prend une maison somptueusement meublée, avec beaucoup de domestiques et se fait conduire dans Paris avec une voiture tirée par quatre ou six chevaux. Il passe son temps en compagnie de beaux esprits, de femmes et de joueurs (comme son travail sur les probabilités le montre. Il poursuit un temps ses travaux en Auvergne, alors qu'il y poursuit aussi de ses assiduités une dame de grande beauté, qu’il appelle la « Sapho de la campagne. À cette époque, il inspire un Discours sur les passions de l’amour (qui ne semble pas être de sa main), et apparemment il a médité sur le mariage qu’il décrit plus tard comme« la plus basse des conditions de la vie permises à un chrétien ».
Jacqueline lui reproche sa frivolité et prie pour qu’il change de vie. Durant les visites à sa sœur à Port-Royal en 1654, il montre du mépris pour les affaires du monde mais il n’est pas attiré par Dieu.
À la fin de 1654, il a un accident sur le pont de Neuilly où les chevaux plongent par-dessus le parapet et la voiture est près de les suivre. Heureusement, l’attelage se rompt et la voiture reste en équilibre sur le bord du pont. Pascal et ses amis sortent, mais le philosophe hypersensible, terrifié par la proximité de la mort, s’évanouit et reste inconscient. Revenant à lui quinze jours plus tard, le 23 novembre 1654, entre dix heures et demie et minuit et demie, Pascal a une intense vision religieuse qu’il écrit immédiatement pour lui-même en une note brève, appelé le Mémorial en littérature, commençant par : Feu. Dieu d’Abraham, Dieu d’Isaac, Dieu de Jacob, pas des philosophes ni des savants… et qu’il conclut par une citation du Psaume 119 : Je n’oublierai pas ces mots. Amen. Il coud soigneusement ce document dans son manteau et le transfère toujours quand il change de vêtement ; un serviteur le découvrira par hasard après sa mort. Pendant sa vie, Pascal a souvent été considéré par erreur comme un libertin et, plus tard, il a été tenu à l’écart comme une personne n’ayant eu une conversion que sur son lit de mort.
Sa croyance et son engagement religieux réactivés, Pascal loge dans le plus ancien des deux couvents de Port-Royal pour une retraite de quinze jours en janvier 1655. Pendant les quatre années suivantes, il fit régulièrement le voyage entre Paris et Port-Royal des Champs. Il commence à écrire, peu après sa conversion, Les Provinciales. Pascal participa aux travaux de traduction en français de la Bible par Louis-Isaac Lemaistre de Sacy.
Vie scientifique Contributions aux mathématiques
Le triangle de Pascal
Dès l'âge de seize ans, il commence à travailler sur ce qui deviendra plus tard la géométrie projective. Il utilise et approfondit les travaux du Brouillon-project d'une atteinte aux evenemens des rencontres du cone avec un plan de Girard Desargues ainsi que ceux d'Apollonius. Ainsi, en 1640, il fait imprimer son Essai pour les coniques et achève, en 1648, un traité de la Generatio conisectionum Génération des sections coniques, dont il ne reste que des extraits pris par Leibniz. La grande innovation est le théorème de Pascal qui dit que l’hexagramme formé par 6 points d’une conique a ses côtés opposés concourants en trois points alignés.
À partir de 1650, Pascal s’intéresse au calcul infinitésimal et, en arithmétique, aux suites de nombres entiers. Les recherches du Traité du triangle arithmétique de 1654 constituent une importante préparation du travail de Leibniz sur le calcul infinitésimal et il y utilise pour la première fois le principe du raisonnement par récurrence. Le formalisme, auquel il recourt assez peu, est plus proche de celui de François Viète et de Francesco Maurolico15 que de Descartes.
Dans ce Traité du triangle arithmétique il donne une présentation commode en tableau des coefficients du binôme, le « triangle arithmétique, maintenant connu sous le nom de triangle de Pascal. Yang Hui, mathématicien chinois sous la dynastie Qin, avait travaillé quatre siècles plus tôt sur un concept semblable ainsi qu'Omar Khayyam au XIe siècle.Il utilise ce tableau arithmétique afin de résoudre le problème des partis, discuté depuis le XIVe siècle. Ce problème, qui lui a été soumis par son ami le chevalier de Méré, concernait le partage équitable des gains d'un jeu de hasard interrompu : deux joueurs décident d’arrêter de jouer avant la fin du jeu et souhaitent partager les gains de manière équitable en s’appuyant sur les chances que chacun avait de gagner une fois à ce point. Pascal correspond alors avec Fermat, d'abord par l'intermédiaire de Carcavi, et cette confrontation de leurs méthodes qui aboutissent à un même résultat le renforce dans l'idée qu'il a réussi à inventer une géométrie du hasard.
Le talent de Pascal, nourri de son expérience de géomètre et de juriste, a été de voir se dessiner la possibilité d'une mathématique du hasard, proprement un oxymore à son époque, et d'avoir approché ainsi la question des décisions équitables et justes, fondamentalement d'ordre juridique. Mis au courant de ces travaux au cours d'un voyage à Paris en 1655, Christian Huygens rédige alors le premier traité sur le calcul des chances, le De ratiociniis in ludo aleae Sur le calcul dans les jeux de hasard, 1657, ou des probabilités, dans lequel il introduit explicitement la notion d'espérance, plus précisément de valeur de l'espérance d'une situation d'incertitude.
Ce travail mathématique sera utilisé à des fins théologiques, dans ce qu'on appelle le pari de Pascal, évoqué dans Les Pensées. Celui-ci suggère l'avantage de la croyance en Dieu et de la pratique des vertus. Cet argument repose sur une utilisation de son calcul du problème des partis permettant d'évaluer le poids probable (son espérance dira Huygens d'une situation incertaine et ainsi de prendre une décision rationnelle. On ne peut dire avec certitude si Pascal a choisi cette approche pour susciter habilement l'intérêt de nobles sceptiques en religion, mais rompus aux jeux de hasard, ou comme fondement effectif d'une théorie des comportements.
Après l’expérience mystique de 1654, Pascal abandonne presque complètement tout travail de mathématique. Il envisage un temps de publier un Promotus Apolloniis Gallus sur le mode de ce qu'avait réalisé François Viète, mais le manuscrit s'en est égaré.
Ses derniers travaux scientifiques concernent les cycloïdes. Cependant, en 1658, il offre anonymement un prix pour la résolution de la quadrature du cercle et la rectification de la cycloïde et autres problèmes liés. Des solutions sont proposées par Wallis, Huygens, Wren et d’autres ; Pascal, sous le pseudonyme de Dettonville, publie alors très vite sa propre solution Histoire de la roulette (en français et en latin avec une Suite de l’histoire de la roulette à la fin de l’année. En 1659, sous le même pseudonyme, il envoie à Huygens une Lettre sur la dimension des lignes courbes.
Pascal savant Physique
L'œuvre de Pascal en physique porte seulement sur la pneumatique et l' hydrostatique et, en outre, elle y est restreinte aux concepts et principes de base. Elle n'en est pas moins de grande portée, pour une double raison : d'abord Pascal a clarifié, approfondi et justifié, par des expériences particulièrement probantes, les conceptions nouvelles qui avaient été dégagées depuis la fin du XVIe siècle, mais qui, jusque-là, demeuraient assez incertaines et de ce fait très controversées ; toutefois, contrairement à une opinion encore assez commune, on ne doit pas à Pascal de contribution tout à fait originale en ce qui concerne ces conceptions elles-mêmes. Ensuite, Pascal a traité ces questions avec une logique, une rigueur, une exigence intransigeantes ne lui faisant reconnaître pour valable que ce qui était vérifié par le contrôle de l'expérience. Cette attitude a joué un rôle décisif dans l'avènement de la méthode « positive » et expérimentale qui caractérise la science moderne.
Pour la majorité des contemporains de Pascal, qu'ils soient aristotéliciens ou cartésiens, le vide n'existe pas. La nature a horreur du vide. Mais, dès 1638, Galilée avait attiré l'attention sur le fait, récemment reconnu, que l'eau ne pouvait s'élever dans une pompe au-delà d'une certaine limite. En 1643, Torricelli, disciple de Galilée, pensant que cette observation n'est pas compatible avec la négation du vide, imagine l'expérience suivante : il retourne un long tube rempli de mercure sur une cuve contenant également du mercure. Il constate que le mercure s'arrête à un niveau équivalant en poids à la colonne d'eau de hauteur maximale dans les pompes. Mieux que ses prédécesseurs, Pascal comprend que cette expérience implique non seulement l'existence du vide, mais aussi la pesanteur de l'air. Niée assez habituellement jusque-là, la pesanteur de l'air a été presque acceptée par Galilée et Baliani, puis par Torricelli à la suite de ses expériences ; elle a été plus nettement affirmée par Isaac Beeckmann, et le chimiste Jean Rey en a apporté la preuve en montrant que des métaux chauffés dans l'air augmentent de poids. Après diverses expériences déjà assez probantes, Pascal fait exécuter, le 19 septembre 1648, par son beau-frère, Florian Périer, en la prescrivant dans tous ses détails, l'expérience du puy de Dôme qui confirme de façon décisive l'existence du vide en même temps que la pesanteur de l'air : le mercure s'abaisse dans le tube à mesure que l'on s'élève. Fort de ces résultats, Pascal rédige, entre 1651 et 1653, un Traité de la pesanteur de la masse de l'air. Mais ce traité n'est que le corollaire d'un ouvrage rédigé à la même époque, le Traité de l'équilibre des liqueurs. Celui-ci rassemble en une doctrine cohérente des acquisitions récentes, essentiellement celles qui se formulent par le « paradoxe de l'hydrostatique », déjà soupçonné par Benedetti en 1585 et nettement reconnu par Stevin en 1596, de même que par Galilée en 1612 : la force qui s'exerce sur le fond d'un vase ne dépend que du poids de la colonne de liquide qui le surmonte à la verticale. Pour un liquide donné, et pour une même hauteur de la surface du liquide au-dessus du fond, ce poids reste le même quelle que soit la forme du vase. Mais Pascal a le mérite de compléter cette théorie en formulant le premier le principe de la presse hydraulique, rattaché à une loi générale de l'hydrostatique qu'il applique aux deux pistons : l'égalité des produits de chaque poids par son déplacement.
Géométrie
À part la géométrie infinitésimale qui sera évoquée plus loin, l'œuvre de Pascal porte essentiellement sur ce qui devait être qualifié plus tard de géométrie projective ; c'est surtout les coniques qu'il a envisagées de ce point de vue. Un texte très bref, Essay pour les coniques, est publié par Pascal, âgé de seize ans, en 1640. Suit un grand Traité des sections coniques dont seul nous est parvenu le premier chapitre, « Generatio conisectionum », les autres parties ne nous étant connues que par des indications de Leibniz qui avait eu l'ouvrage en main.
On sait que la vocation de Pascal pour la géométrie s'éveilla quand il eut douze ans, à la lecture des Éléments d'Euclide. Mais c'est seulement en 1639 qu'il commença à s'y intéresser de façon sérieuse. Il eut alors connaissance du court ouvrage du géomètre architecte Girard Desargues, Brouillon project d'une atteinte aux événements des rencontres du cône avec un plan, qui venait de paraître. Cette œuvre capitale jetait les bases de la géométrie projective et d'une théorie unitaire des coniques. Le jeune Blaise Pascal fut alors seul à en comprendre toute la richesse. Il en adopta aussitôt les idées fondamentales : introduction des éléments à l'infini, définition des coniques comme sections planes quelconques de cônes à base circulaire, étude de ces courbes comme perspectives du cercle, relation d'involution déterminée sur une droite quelconque par une conique et les côtés d'un quadrilatère inscrit. Mais bientôt Pascal prolonge les idées de Desargues par un apport original. Dès 1639, il démontre son célèbre théorème : les points d'intersection des couples de côtés d'un hexagone inscrit dans une conique sont en ligne droite (cf. coniques, chap. 1). Il rédige alors l'Essay pour les coniques. Il utilise l'œuvre d'Apollonius, qui, dans son ouvrage sur les coniques, avait notamment défini les propriétés des diamètres et des tangentes, mais il énonce ces résultats d'une manière plus universelle qu'à l'ordinaire.
Il faut aussi noter des travaux, dont certains seulement se rattachent à la géométrie projective, et où, sans avoir fourni des contributions aussi originales, Pascal a atteint des résultats notables : contacts circulaires, contacts sphériques, et surtout lieux plans, c'est-à-dire les lieux géométriques exclusivement formés de droites et de cercles, et lieux solides, c'est-à-dire les lieux formés de coniques, qui occupent déjà une large place chez Apollonius ainsi que dans la collection mathématique de Pappus. Parmi les problèmes des lieux solides, le plus célèbre est alors celui dit de Pappus, qui fait intervenir quatre droites du plan et l'égalité de produits de segments. Ce problème avait été l'arme principale de Descartes pour établir l'excellence de sa géométrie analytique. Mais la géométrie analytique ne devait pas retenir l'attention de Pascal. Il traite ce problème de façon purement géométrique, liant étroitement sa solution à sa méthode d'étude projective des coniques, dont il prouvait ainsi la puissance et la fécondité.
Si remarquables qu'elles fussent, les vues de Pascal sur la géométrie projective eurent peu d'échos. Leibniz en reconnut l'intérêt, mais ne les exploita pas, et l'ouvrage de Philipe de La Hire, Nouvelle Méthode en géométrie, publié en 1673 et qui s'appuie sur elles, n'eut qu'une faible diffusion.
C'est seulement au XIXe siècle, avec le Traité des propriétés projectives des figures de Poncelet (1822), que devait être pleinement reconnue la portée de l'œuvre géométrique de Pascal (cf. géométrie, chap. 3).
Posté le : 18/06/2016 21:25
|
|
|
|
|
Blaise Pascal 2 |
|
Administrateur  
Inscrit:
14/12/2011 15:49
De Montpellier
Niveau : 63; EXP : 94
HP : 629 / 1573
MP : 3168 / 60051
|
L'analyse infinitésimale
Pascal occupe une place centrale dans l'histoire de l'analyse infinitésimale. Ses travaux sur ce sujet se situent environ entre 1650 et 1660, donc dans les dernières années de sa vie, et s'appuient sur ceux, un peu antérieurs, de Stevin, Descartes, Roberval, Torricelli, Grégoire de Saint-Vincent et Tacquet. Ils sont à peu près contemporains de ceux de Fermat, qui compte d'ailleurs parmi ses principaux correspondants. Ils précèdent ceux de Leibniz et de Newton qui lui devront beaucoup.
Pascal fait progresser les conceptions de base de ce calcul, qu'il trouve encore assez incertaines, et il obtient plusieurs résultats de grande portée. Mais il n'a pas recours au symbolisme et aux signes opératoires de l'algèbre, cependant déjà assez développée et répandue, à la suite notamment des travaux de Viète, Descartes et Fermat. Il demeure attaché au langage géométrique et éventuellement mécanique, ce qui ne l'empêche pas d'atteindre des résultats d'une grande généralité, mais dont l'exposé se trouve souvent assez lourd.
La notion d' indivisible, à la base du calcul infinitésimal, avait donné lieu à maintes discussions souvent stériles, mais elle avait été utilisée de façon renouvelée par Cavalieri qui avait montré qu'elle offrait une méthode générale pour la sommation des surfaces et des volumes, méthode supérieure à celle d'exhaustion des Anciens. Pascal débarrasse cette notion des obscurités et de la « métaphysique » dont elle était encore chargée ; il use notamment du passage à la limite de façon systématique, ayant soin d'en justifier la légitimité, ce dont on n'avait guère eu le souci avant lui.
La contribution de Pascal au calcul infinitésimal porte surtout sur l' intégration. Avant lui, plusieurs mathématiciens, principalement Cavalieri et Fermat, avaient trouvé la formule d'intégration de xm pour m entier positif. Fermat avait même étendu la formule à tout m rationnel différent de − 1. Mais Pascal donne de cette formule, pour m entier positif, une démonstration particulièrement claire et qui repose, pour la première fois, sur un passage à la limite à partir des formules donnant les sommes des puissances semblables de la suite des nombres entiers.
Pascal a en outre le mérite d'envisager le premier le problème général de l'intégration d'une fonction quelconque, conçue par lui comme un arc de courbe formant avec les deux axes de coordonnées un triligne rectangle. À la vérité, cette question avait été déjà abordée en 1647 par le jésuite Grégoire de Saint-Vincent qui avait établi des relations générales entre intégrales. Mais Pascal, qui connaît les travaux de Saint-Vincent, la formule de manière beaucoup plus claire et étend les résultats qu'il obtient, en les appliquant notamment au calcul des centres de gravité. On notera toutefois une faiblesse dans ses travaux : Pascal ne considère que la division de l'axe des x en parties égales.
Un autre apport notable de Pascal au calcul infinitésimal est l'introduction de la notion de triangle caractéristique, triangle rectangle dont les côtés de l'angle droit sont les accroissements dx et dy qui, d'abord finis, peuvent devenir infiniment petits. Mais Pascal ne considère que le triangle caractéristique lié au cercle. Reprenant cette notion, Leibniz le premier l'envisagera dans le cas d'une courbe quelconque.
Pascal a appliqué ces méthodes à de nombreux problèmes, ainsi les propriétés de la roulette (la cycloïde), qui occupait alors la plupart des mathématiciens. Il obtint des résultats remarquables et particulièrement élégants en ce qui concerne notamment la longueur de l'arc de cette courbe ainsi que la surface et le centre de gravité de l'aire qu'elle délimite avec l'axe des x.
Arithmétique
La théorie des nombres entiers dans ses aspects les plus fondamentaux (équations en nombres entiers, propriétés des nombres premiers) ne doit aucun progrès à Pascal, alors que son contemporain et correspondant Fermat y a apporté une brillante contribution. Mais Pascal s'est intéressé aux propriétés des suites de nombres entiers, qualifiés par lui ordres numériques : nombres naturels, nombres triangulaires (sommes des précédents), nombres pyramidaux (sommes des nombres triangulaires). Rangées par lignes superposées, ces suites forment le triangle arithmétique, qui possède d'intéressantes propriétés. Toutefois, ce dernier n'est pas une invention de Pascal. On le rencontre déjà chez Stifel en 1543. Mais Pascal le premier en fit une étude systématique, et cela dans plusieurs écrits, surtout dans son Traité du triangle arithmétique (1654). Il l'appliqua à l'étude des ordres numériques, au calcul des coefficients du développement des puissances entières du binôme, à l'établissement de la formule donnant le nombre de combinaisons de n objets p à p, enfin au problème des partis dont il sera question plus loin. Sauf pour cette dernière application, sa contribution est assez peu originale. Toutefois, au cours de plusieurs démonstrations, notamment l'établissement de la formule des combinaisons, Pascal utilise le premier la méthode de la démonstration dite par récurrence, ou encore induction mathématique, dont on sait le rôle majeur dans la mathématique moderne.
Les probabilités, les partis
C'est à bon droit que l'on peut accorder à Pascal le mérite d'avoir fondé le calcul des probabilités. Avant lui, sans doute, les jeux de hasard, les risques des opérations commerciales et leur légitimité morale avaient donné lieu à nombre de considérations où se dessinait une amorce de théorie. Mais Pascal le premier aborde ces sujets de façon générale et mathématique, et cela à l'occasion du problème des partis qu'il traite dans son ouvrage sur le triangle arithmétique ainsi que dans un important échange de lettres avec Fermat. Il utilise de façon très ingénieuse les formules combinatoires qu'il a établies à partir des propriétés du triangle arithmétique. Mais sa contribution la plus remarquable réside dans la doctrine qu'il met à la base de la solution de ce problème et qui, à la lumière des vues modernes sur la théorie de la décision, nous apparaît comme la première prise en considération sérieuse et rationnelle du parti à prendre en face d'un avenir incertain. En très bref, le problème des partis peut s'énoncer ainsi : deux joueurs décidant d'arrêter une partie avant son achèvement, il s'agit de déterminer comment l'enjeu restant doit être réparti entre eux. Chaque joueur prendra d'abord la somme minimale qui lui reviendrait quoi qu'il advienne. Quant à la somme restante, elle sera partagée par moitié s'il y a « autant de hasards » que l'un des joueurs gagne que l'autre, si la partie est continuée. Ainsi Pascal détermine une manière de faire « certaine » en face de l'incertitude. Aussi pouvait-il déclarer dans les Pensées que l'on « travaille pour l'incertain sur mer, en bataille », mais qu'avant lui on « n'a pas vu la règle des partis qui démontre qu'on le doit ».
La machine arithmétique
Seule contribution de Pascal au progrès des sciences appliquées, la machine arithmétique est une réalisation profondément novatrice. Par l'ingéniosité de sa conception, les soins apportés à sa réalisation effective, puis à sa diffusion, cette machine constitue le point de départ de dispositifs qui, par une série de perfectionnements, devaient conduire aux calculatrices électromécaniques et électroniques modernes.
À Rouen, en 1640, Pascal envisagea de construire une machine effectuant les quatre opérations arithmétiques élémentaires. Son objectif était de faciliter les pénibles opérations comptables dont son père avait la charge.
Surtout depuis le début du XVIIe siècle, l'accroissement et la complexité des opérations numériques qui résultaient du développement aussi bien de l'algèbre et de l'astronomie que des opérations commerciales et bancaires avaient conduit à la création, en plus des systèmes de jetons et de bouliers d'usage ancien, de réglettes utilisant les logarithmes récemment inventés par John Napier. Chronologiquement, la première machine effectuant les quatre opérations n'est pas due à Pascal, mais à l'astronome allemand Wilhelm Schickard 1592-1635. Il l'a réalisée autour de 1622. Elle était constituée par une additionneuse mécanique associée à un ensemble de cylindres népériens destinés à la multiplication, la division et l'extraction de racines carrées. Mais cette machine n'eut aucune diffusion et il ne semble pas qu'elle était effectivement utilisable. En tout cas, Pascal n'a eu aucune connaissance de cette invention, et, alors que la machine de Schickard n'est mentionnée que dans deux lettres de Kepler, celle de Pascal est citée et décrite par de nombreux témoins, et plusieurs exemplaires d'époque sont parvenus jusqu'à nous.
Pascal a tenu à préciser que c'est d'un point de vue théorique que, vers la fin de 1640, il aborda le difficile problème de la mécanisation du calcul. Il se heurta à de grandes difficultés de réalisation ; en 1642, il fut sur le point de renoncer à son projet, mais, encouragé par ses amis, il se remit à la tâche ; en 1645, il put offrir au chancelier Séguier une machine au fonctionnement correct. Préoccupé de l'exploitation de son invention, Pascal rédige la même année une note publicitaire qui en vante les qualités, et il en entreprend la construction en petite série. Par privilège royal, il obtient en 1649 le bénéfice exclusif de sa fabrication et de sa vente. Mais le prix très élevé cent livres devait limiter le nombre des acheteurs.
La machine est composée de six étages, correspondant aux six ordres d'unités traitées. L'organe essentiel de chaque étage est une roue à dix dents. La mécanisation de l'opération de report, qui doit relier les étages consécutifs, faisait avancer l'étage supérieur au moment où l'étage inférieur passe de 9 à 0 est assurée par un dispositif assez complexe fonctionnant sous l'effet de la pesanteur.
De nombreux inventeurs suivirent la voie ouverte par Pascal. Plusieurs types d'additionneuse furent mis au point au XVIIe et au XVIIIe siècle, mais elles furent peu utilisées. C'est seulement au XIXe siècle que le calcul mécanique prit une réelle extension.
Si l'on doit attribuer à Schickard la première mécanisation des opérations arithmétiques, fondée essentiellement sur l'emploi d'une roue dentée, c'est Pascal qui, le premier, formula les principes du calcul mécanique, mit en lumière la structure générale des machines arithmétiques et triompha des difficultés techniques auxquelles se heurtait sa réalisation. François Russo
Philosophie des mathématiques Axiomatique
La contribution majeure de Pascal à la philosophie des mathématiques est De l’Esprit géométrique, écrit originellement comme une préface d’un manuel Éléments de géométrie pour les célèbres petites-écoles de Port-Royal, à la demande d’Arnauld. Ce travail n’a été publié qu’un siècle après sa mort. Pascal y examine les possibilités de découvrir la vérité, argumentant que l’idéal pour une semblable méthode serait de se fonder sur les propositions dont la vérité est déjà établie. Toutefois, il affirmait que c’était impossible parce que pour établir ces vérités, il faudrait s’appuyer sur d’autres vérités et que les principes premiers ne pourraient être atteints. De ce point de vue, Pascal affirmait que la procédure utilisée en géométrie était aussi parfaite que possible, avec certains principes énoncés mais non démontrés et les autres propositions étant développées à partir d’eux. Néanmoins, il n’existait pas de possibilité de savoir si ces principes étaient vrais.
Dans De l’Esprit géométrique et de l’Art de persuader, Pascal étudie plus encore la méthode axiomatique en géométrie, particulièrement la question de savoir comment le peuple peut être convaincu par les axiomes sur lesquels les conclusions sont fondées ensuite. Pascal est d’accord avec Montaigne qu’obtenir la certitude à propos de ces axiomes et des conclusions grâce aux méthodes humaines était impossible. Il assurait que ces principes ne pouvaient être saisis que par l’intuition et que ce fait soulignait la nécessité de la soumission à Dieu dans la recherche de la vérité.
Dans De l’Esprit géométrique et de l’Art de persuader, Pascal fait l’épistémologie des mathématiques. Les mathématiques reposent d’abord sur des principes évidents connus par intuition malheureusement, Pascal comme Descartes ignore ce mot et le remplace par : cœur, sentiment ou instinct. Il serait vain de vouloir démontrer ces principes évidents en utilisant des affirmations moins évidentes. Mais les mathématiques reposent aussi sur des principes conventionnels, non évidents, non démontrés, et qui une fois admis, ont autant de force que les précédents ce qui ouvrait la porte aux géométries non-euclidiennes.
Pascal développe aussi dans De l’Esprit géométrique… une théorie de la définition. Il distingue les définitions qui sont des termes conventionnels définis par l’auteur et les définitions incluses dans le langage et comprises par tous parce qu’elles désignent naturellement leur référent. Les secondes sont caractéristiques de la philosophie de l’essence essentialisme. Pascal affirme que seules les définitions du premier type sont importantes pour la science et les mathématiques, considérant que ces domaines devraient adopter la philosophie du formalisme, comme Descartes l’a établie.
Pédagogie
Pascal montre dans ces Éléments de géométrie tout son intérêt pour l’enseignement et ses réflexions à propos de la pédagogie des mathématiques et aussi dans un autre fragment, connu par l’intermédiaire de Leibniz, sur une méthode de lecture qu’il a discuté avec sa sœur Jacqueline, chargée d’enseigner dans les petites-écoles de Port-Royal. Il a semble-t-il lui-même enseigné, chez lui, à plusieurs enfants en loques d’après Villandry. Dans cette méthode de lecture, qu’il présente comme Une nouvelle manière pour apprendre à lire facilement en toutes sortes de langues, il recommande :
Cette méthode regarde principalement ceux qui ne savent pas encore lire. ... chaque lettre ayant son nom, on la prononce seule autrement qu’en l’assemblant avec d’autres. ... Il semble que la voie la plus naturelle ... est que ceux qui montrent à lire, n’apprissent d’abord aux enfants à connaître les lettres, que par le nom de leur prononciation.
Pascal donne des indications sur l’ordre de présentation des lettres et des divers cas avec ou sans diphtongue, etc.
Et ensuite on leur apprendrait à prononcer à part, et sans épeler, les syllabes ce, ci, ge, gi, tia, tie, tii...
Contributions aux sciences physiques
Expérience des liqueurs
Statue de Pascal sous la Tour Saint-Jacques à Paris où il aurait répété ses expériences du puy de Dôme sur la pression atmosphérique et la pesanteur de l'air.
Blaise Pascal a également réalisé la fameuse expérience des liqueurs (qu’on traduirait aujourd’hui par Expérience des liquides), qui prouva qu’il existait une « pression atmosphérique ». À l’époque, (où la science était encore très liée à la scolastique et à Église) l’idée était courante selon laquelle « la nature a horreur du vide ». La plupart des scientifiques supposaient que quelque invisible matière remplissait cet espace, mais que ce n’était pas un espace vide. Des inondations ayant eu lieu en Italie et en Hollande avaient conduit à des pompages d’eau pour vider les carrières de minerai des deux pays. Mais les pompes énormes fabriquées pour l’occasion laissaient perplexes les hommes de l’Église : la hauteur de l’eau dans les tubes de pompage s’arrêtait à 10,33 m. Et cela en des lieux très différents. À Clermont, Blaise Pascal est en train d’écrire un traité sur la mécanique des fluides. Il émet donc l’hypothèse qu’une sorte de « pression atmosphérique » empêche l’eau de monter très haut dans les pompes, et que le vide occupe l’espace supérieur des tubes. Cependant, il se heurte fortement à certains esprits de son temps et particulièrement à l'Église, qui fait refaire l’étanchéité des pompes afin de vérifier qu’il ne s’agit pas d’air. Mais leurs travaux leur donnent finalement tort.
Blaise Pascal répète, en 1646 avec son père à Rouen, les expériences de Torricelli sur le vide. Un procès verbal en est envoyé à leur ami Chanut ambassadeur du Roi en Suède. En 1647, Pascal publie ses Expériences nouvelles touchant le vide et une préface pour un Traité du Vide, voir aussi vide dans le vide de, où il détaille les règles de base décrivant à quel degré les divers liquides pouvaient être maintenus par la pression de l’air. Il fournit aussi les raisons pour lesquelles un vide se trouvait réellement au-dessus de la colonne de liquide dans le tube barométrique.
Il a alors l’idée d’une expérience qu’il va réaliser le 19 septembre 1648 : la pression atmosphérique devrait être différente en ville à Clermont et en haut de la montagne la plus proche, le Puy de Dôme, où la pression doit être inférieure à la pression régnant au niveau de la ville. Pascal fait donc transporter par son beau-frère, Florin Périer, un tube de Torricelli en haut du Puy-de-Dôme. Des curés et des savants suivent l’expérience. Grâce au tube-témoin en ville, la présence de vide est démontrée. Il publie le Récit de la grande expérience de l’équilibre des liqueurs.
Ce travail de recherche se termine en 1651 par un Traité du vide seuls des fragments en sont connus et sa réduction par Pascal en deux traités de l’Équilibre des liqueurs et de la Pesanteur de l’air. C’est en septembre de cette année que son père Étienne meurt.
Le travail de Pascal dans l’étude des fluides hydrodynamique et hydrostatique est centré sur les principes des fluides hydrauliques. Il invente le principe de la presse hydraulique dénommé à l'époque principe du vaisseau d'eau, utilisant la pression hydraulique pour multiplier la force et la seringue.
Face aux critiques qui soutenaient que quelque matière invisible existait dans l’espace vide de Pascal, Pascal répondit à Étienne Noël par un des principes fondateurs de la méthode scientifique au XVIIe siècle :
Pour montrer qu’une hypothèse est évidente, il ne suffit pas que tous les phénomènes la suivent ; au lieu de cela, si elle conduit à quelque chose de contraire à un seul des phénomènes, cela suffit pour établir sa fausseté.
Son insistance sur l’existence du vide le place, aussi, en conflit avec de nombreux scientifiques éminents, y compris Descartes peut-être aussi et surtout pour des raisons religieuses.
Écrivain, philosophe ou théologien de la maturité
Les Provinciales
Antoine Arnauld, chef de file des jansénistes depuis la mort de Jean Duvergier de Hauranne, était en désaccord avec la Sorbonne au sujet d’une bulle d’Innocent X, mai 1653. Cherchant à défendre l’un de ses amis, le marquis de Liancourt, il s’attira les foudres de la Sorbonne. Les jansénistes cherchèrent un défenseur en la personne de Pascal.
Pascal accepta, assurant qu’il savait selon Sainte-Beuve comment on pourrait faire ce factum », mais qu’il ne pouvait promettre qu’une ébauche que d’autres se chargeraient de polir. Pascal commença à publier les lettres à partir du 23 janvier 1656 sous le pseudonyme de Louis de Montalte. Pascal lança une attaque mémorable contre la casuistique, une méthode morale populaire chez les penseurs catholiques, particulièrement les jésuites. Pascal dénonça la casuistique comme l’utilisation d’un raisonnement complexe pour justifier une morale laxiste. Sa méthode pour argumenter fut subtile : les Provinciales prétendaient être les Lettres écrites par Louis de Montalte à un provincial de ses amis et aux R.R.P.P. révérends pères Jésuites sur le sujet de la morale et de la politique de ces pères. Il s’adresse à un ami qui vit en province à propos des discussions sur la morale et la théologie qui excitaient les cercles intellectuels et religieux de la capitale, particulièrement la Sorbonne. Pascal allia la ferveur d’un nouveau converti et l’esprit brillant d’un homme du monde, avec un style de la prose française inconnu jusque là. À côté de leur influence religieuse, Les Provinciales ont été une œuvre littéraire populaire. Pascal se servit de l’humour, de la moquerie et de la satire méchante dans ses arguments, pour permettre une utilisation publique des lettres qui influenceront plus tard des écrivains français comme Voltaire, Jean-Jacques Rousseau, et surtout le Montesquieu des Lettres persanes.
Les premières lettres défendent la position des jansénistes contre leurs adversaires jésuites ou dominicains, homistes, sur les questions du pouvoir prochain Lettre I, de la grâce efficace ou suffisante Lettre II, de la possibilité que la grâce puisse manquer à un juste Lettre III. À partir de la quatrième lettre, Pascal passe à l'offensive. Ses attaques contre les autorités prennent, selon Jean Lacouture, un ton polémique tel que Voltaire lui-même n’a jamais peut-être atteint à cette fulgurance : il nomma personnellement et par écrit un grand nombre de personnalités. Les dernières lettres montrent Pascal davantage sur la défensive – les pressions sur les jansénistes de Port-Royal pour qu’ils renoncent à leur enseignement sont croissantes pendant ce temps – et contiennent l’attaque contre la casuistique. La Lettre XIV présente une seule excuse : Je voudrais avoir écrit une lettre plus courte, mais je n’en ai pas le temps.
La série de dix-huit lettres, publiées entre 1656 et 1657 par Pierre Le Petit, choque Louis XIV, qui a commandé en 1660 que le livre soit déchiqueté et brûlé. En 1661, l’école janséniste de Port-Royal était condamnée à son tour et fermée, ceci aboutissant à la signature d’une bulle papale condamnant l’enseignement des jansénistes comme hérétiques. La dernière lettre défiait le pape lui-même, provoquant Alexandre VII à condamner les lettres le 6 septembre 1657. Mais ceci n’empêcha pas la France cultivée de les lire.
Le pape Alexandre VII, alors qu’il s’opposait publiquement à elles, était convaincu par les arguments de Pascal. Il ordonna une révision des textes casuistiques juste quelques années après, en 1665 et 1666. Le pape Innocent XI condamna le laxisme dans l’Église en 1679.
Les Provinciales ont été largement diffusées dès leur parution, à plus d’une dizaine de milliers d’exemplaires.
Voltaire les a jugées le meilleur livre qui ait jamais paru en France, et quand on a demandé à Jacques-Bénigne Bossuet quel livre il aurait aimé écrire, il a répondu, Les Provinciales de Pascal.
Jean Lacouture Jésuites cite d’autres appréciations, celles d’Henri Gouhier et de François Mauriac.
Au sujet de l’impact qu’eurent les Provinciales dans leur contexte historique, Jean Lacouture cite l’historien Marc Fumaroli (voir Révolution copernicienne : Réaction des scientifiques : Pascal.
Les Pensées
Dans Pensées 1669, Pascal introduit la notion d'ordre comme un ensemble homogène et autonome, régi par des lois, se rangeant à un certain modèle, d'où dérive son indépendance par rapport à un ou plusieurs autres ordres. Les trois ordres identifiés par Pascal sont l'ordre du corps, l'ordre de l'esprit ou de la raison, et l'ordre du cœur ou de la charité. Cette notion d'ordre a été reprise par le philosophe André Comte-Sponville.
Postérité
La Pascaline. Hommages
En l’honneur de ses contributions scientifiques, le nom de pascal a été donné à l’unité de pression du système international, à un langage de programmation et à la loi de Pascal un principe important d’hydrostatique et, comme mentionné ci-dessus, le triangle de Pascal et le pari de Pascal portent toujours son nom.
Le développement de la théorie des probabilités est la contribution de Pascal la plus importante en mathématiques. À l’origine appliquée au jeu, elle est aujourd’hui utilisée dans les sciences économiques, particulièrement en science actuarielle. John Ross écrit :
La théorie des probabilités et les découvertes qui la suivent ont changé la manière dont nous considérons l’incertitude, le risque, la prise de décision, et la capacité d’un individu ou de la société d’influencer le cours d’événements futurs.
Machine arithmétique de Pascal - L’Encyclopédie.
Cependant, il convient de noter que Pascal et Fermat, qui effectuent les premiers travaux importants en théorie des probabilités, n’ont pas développé très loin ce champ d’études. Christian Huygens, étudiant la question en 1655 à partir de ouï-dire à propos de la correspondance entre Pascal et Fermat, a écrit le premier livre sur le sujet. Jacques Bernoulli, Pierre Rémond de Montmort, Abraham de Moivre, Thomas Bayes, Nicolas de Condorcet et Pierre-Simon de Laplace sont, parmi les auteurs qui ont prolongé le développement de la théorie, ceux dont la contribution a été la plus importante au XVIIIe siècle .
Au Canada, un concours annuel de mathématiques est appelé en son honneur Concours Pascal qui est ouvert à n’importe quel élève du Canada de moins de 14 ans et en 9e au plus.
En informatique, le Pascal est un langage de programmation créé par Niklaus Wirth et nommé en l'honneur de Blaise Pascal.
L’Université Clermont-Ferrand II a été baptisée à son nom et édite les Annales Mathématiques Blaise Pascal, et le nom a également été donné à une université de Cordoba en Argentine.
La Banque de France a émis un billet de banque, le 500 francs Pascal, sa plus haute coupure de 1969 à 1994, à son effigie.
En 1964, l'Union astronomique internationale a donné le nom de Pascal à un cratère lunaire.
Pascal a sa statue parmi les Hommes illustres au musée du Louvre à Paris.
Littérature
En littérature, Pascal est considéré comme un des auteurs les plus importants de la période classique française et il est lu aujourd’hui en tant qu’un des plus grands maîtres de la prose française. Son utilisation de la satire et de l’esprit a influencé des polémistes postérieurs. On se souvient bien de la teneur de son travail littéraire à cause de sa forte opposition au rationalisme de René Descartes et de l’affirmation simultanée que l’empirisme philosophique était également insuffisant pour déterminer des vérités majeures.
Chateaubriand a décrit ses contributions dans une célèbre envolée lyrique se concluant par il fixa la langue que parlèrent Bossuet et Racine, donna le modèle de la plus parfaite plaisanterie, comme du raisonnement le plus fort ... cet effrayant génie se nommait Blaise Pascal .
Jules Barbey d'Aurevilly voit en Pascal un Hamlet du catholicisme . Charles Baudelaire le paraphrase et lui consacre son poème Le gouffre.
Une discussion à propos de Pascal et de son pari occupe une place importante dans le film Ma nuit chez Maud du réalisateur français Éric Rohmer.
La méditation pascalienne sur le divertissement trouve un prolongement dans le roman de Jean Giono, Un roi sans divertissement 1947. Giono emprunte le titre et la dernière phrase du livre à un passage des Pensées fragment 142 de l’édition Brunschvicg : Un roi sans divertissement est un homme plein de misères.
Pour Julien Green, Pascal est « Le plus grand des Français.
Sœur Emmanuelle, dans son livre Vivre, à quoi ça sert ? éditions J’ai Lu s’appuie sur quelques principes de la pensée pascalienne qui fut un guide pour elle, tout au long de sa vie.
Vers la fin de sa vie le sociologue Pierre Bourdieu a publié un livre de réflexions sur son domaine qui est intitulé Méditations pascaliennes.
Œuvres de Pascal Liste des principales œuvres
La chronologie exacte des œuvres de Pascal est difficile à établir car de nombreux textes ne sont pas datés et ont été publiés longtemps après avoir été rédigés. Certains n’ont été connus qu’un siècle ou plus après le décès de Pascal, d’autres ne nous sont parvenus que de manière fragmentaire ou indirecte notes de Leibniz ou correspondance, par exemple.
Essai pour les coniques 1640
Expériences nouvelles touchant le vide 1647
Récit de la grande expérience de l’équilibre des liqueurs (1648
Traité du triangle arithmétique 1654
Les Provinciales Correspondances 1656-1657
Élément de géométrie 1657
De l’Esprit géométrique et de l’Art de persuader 1657
Histoire de la roulette 1658
L’Art de persuader 1660
Pensées (1669, posthume
Abrégé de la vie de Jésus-Christ texte retrouvé vers 1840, publié en 1846
Textes de Pascal
De très nombreuses éditions existent:
Blaise Pascal, Œuvres de Blaise Pascal en 5 tomes, La Haye, Chez Detune, Libraire, 1779.
Blaise Pascal, Pensées de Pascal, précédées de Sa vie, par Mme Perier, sa sœur, Paris, Librairie de Firmin-Didot frères,
Pascal, Œuvres complètes, Louis Lafuma, Seuil, L'Intégral, 1963
Pascal, Œuvres complètes, texte établi, présenté et annoté par Jacques Chevalier. Bibliothèque de la Pléiade. Éditions Gallimard, 1936-1998.
Pascal, Œuvres complètes, éd. Jean Mesnard, Paris, Desclée de Brouwer, 1964-1992, qui contient tous les textes qui intéressent la vie ou l’œuvre de Pascal y compris des actes notariés, etc.. Mais seuls 4 des 7 volumes ont paru à ce jour et ils ne contiennent ni Les Provinciales ni les Pensées.
Pascal, Œuvres complètes, éd. Michel Le Guern, coll. Bibliothèque de la Pléiade, Paris, Gallimard, 2 volumes, 1998 et 2000.
Blaise Pascal, Discours sur la religion et sur quelques autres sujets qui ont été trouvés après sa mort parmi ses papiers, restitués et publiés par Emmanuel Martineau, Paris, Fayard-Armand Colin, 1992.
Blaise Pascal, Pensées, opuscules et lettres, éd. par Philippe Sellier, Paris, Éditions Classiques Garnier, coll. « Bibliothèque du XVIIe siècle », 2010.
Blaise Pascal, Pensées sur la religion et sur quelques autres sujets étude et édition comparative de l'édition originale avec les copies et les versions modernes par Jean-Robert Armogathe et Daniel Blot, Paris, Honoré Champion, 2011.
Commentaires d'écrivains
François-René de Chateaubriand, Mémoires d'outre-tombe, II, Chapitre VI.
François Mauriac, Blaise Pascal et sa sœur Jacqueline, Paris, Hachette, 1931.
Sainte-Beuve, Port-Royal, Hachette, 1860, ;
Paul Valéry, "Variation sur une pensée" 1923, dans Œuvres, I, Bibliothèque de la Pléiade, Paris, Gallimard, 1957, p. 458-473.
Voltaire, Lettres philosophiques 1737, Paris, Flammarion, 2006.
Études d'ensemble, monographies, biographies
Donald Adamson, Blaise Pascal: Mathematician, Physicist, and Thinker about God, Londres et New York, Macmillan, 1995.
Francesco Paolo Adorno, Pascal, Paris, Les Belles Lettres, 2000 .
Vlad Alexandrescu, Le Paradoxe chez Blaise Pascal, Peter Lang, 1997.
Jacques Attali, Blaise Pascal, ou le génie Français, Paris, Fayard, 2000.
Charles Baudouin, Blaise Pascal ou l’ordre du cœur, Paris, Plon, 1962.
Albert Béguin, Pascal, Paris, Seuil, 1952 ; nouvelle éd. 1981.
Hervé Bonnet, Pascaĺ, Bruxelles, Sils-Maria, 2013.
André Bord, Pascal et Jean de la Croix, préface de Philippe Sellier, Paris, Beauchesne, 1987.
André Bord, La Vie de Blaise Pascal, Paris, Beauchesne, 2000.
André Bord, Pascal vu par sa sœur Gilberte, Paris, Pierre Téqui, 2005.
André Bord, Lumière et Ténèbres chez Pascal, Paris, Pierre Téqui, 2006.
Léon Brunschvicg, Blaise Pascal, Paris, J. Vrin, 1953.
Léon Chestov, La Nuit de Gethsémani. Essai sur la philosophie de Pascal, Grasset, 1923.
Jacques Chevalier, Pascal, Libr. Plon, Nourrit et Cie, coll. Les Maîtres de la pensée française, 1922 réimpr. 1944.
Francis X. J. Coleman, Neither Angel Nor Beast: The Life and Work of Blaise Pascal, New York, Londres, Routledge and Kegan Paul, 1986.
Dominique Descotes, Pascal : biographie, étude de l’œuvre, Paris, Albin Michel, 1994.
Gérard Ferreyrolles, Pascal et la raison du politique, PUF, 1984.
Jean-Louis Gardies, Pascal entre Eudoxe et Cantor, Paris, J. Vrin, 1984.
Jonas Geffroy, Blaise Pascal, vie et œuvre Édition Atlas, 2003.
Henri Gouhier, Blaise Pascal : conversion et apologétique, Paris, Vrin, 1986.
Henri Gouhier, Blaise Pascal, commentaires, Paris, Vrin, 1966.
Thomas More Harrington, Pascal philosophe, Paris, CDU-SEDES, 1982
Michel Le Guern, Pascal et Descartes, Nizet, 1971.
Michel Le Guern, Pascal et Arnauld, Paris, Honoré Champion, 2003.
Michel Le Guern, Études sur la vie et les Pensées de Pascal, Paris, Honoré Champion, 2015.
Michel Le Guern, L'Image dans l'œuvre de Pascal, Armand Colin, 1969.
Pierre Magnard, Nature et histoire dans l’apologétique de Pascal, Paris, Belles-Lettres, 1975.
Pierre Magnard, Pascal - La clé du chiffre, La Table ronde, 2007.
Pierre Magnard, Pascal ou l’art de la digression, Ellipses, 1995.
Pierre Magnard, Le Vocabulaire de Pascal, Ellipses, 2001.
Jean Mesnard, Pascal, coll. Connaissance des Lettres, Paris, Hatier, 1967.
Jean Mesnard, Pascal, coll. Les Écrivains devant Dieu, Paris, Desclée de Brouwer, 1965.
Jean Mesnard, Pascal et les Roannez, Paris, Desclée De Brouwer, 1965, 2 vol.
Jean-Félix Nourrisson, Pascal, physicien et philosophe, Paris, Librairie académique Didier, 1885.
Hervé Pasqua, Pascal, penseur de la grâce, Téqui, 2000.
Marguerite Perroy, Les Pascal, un trio fraternel, Editions Letouzey et Ané Paris 1959.
René Pommier, "Ô Blaise! à quoi tu penses?", Essai sur les Pensées de Pascal, Éditions du Comité d'Action laïque, Bruxelles, 2003; réédition éditions Kimé, Paris, 2015.
Maurice Pontet, Pascal et Teilhard, témoins de, Jésus-Christ, Desclée de Brouwer, Paris, coll. Christus no 27, 1968, 221 p.
Philippe Sellier, Pascal et saint Augustin, Paris, Albin Michel, 1995
Philippe Sellier, Essais sur l’imaginaire classique. Pascal - Racine - Précieuses et Moralistes - Fénelon., Paris, Honoré Champion, 2005.
Tetsuya Shiokawa, Pascal et les miracles, Paris, Nizet, 1977
Laurent Thirouin préf. Jean Mesnard, Le Hasard et les règles : le modèle du jeu dans la pensée de Pascal, Vrin, coll. Bibliothèque d’histoire de la philosophie, 1991, 222 p.
Rhétorique de Pascal
Dominique Descotes, L'Argumentation chez Pascal, Paris, PUF, 1993.
Laurent Susini, L’Écriture de Pascal. La lumière et le feu. La vraie éloquence à l’œuvre dans les Pensées, Paris, Honoré Champion, 2008 (prix G. Dumézil de l’Académie française.
Pascal scientifique
Jacques Darriulat, L’Arithmétique de la Grâce : Pascal et les carrés magiques, Paris, les Belles lettres, 1994.
Pierre Guenancia, Du vide à Dieu : essai sur la physique de Pascal, Paris, Maspero, 1976.
Pierre Humbert, L’Œuvre scientifique de Blaise Pascal, Paris, Albin Michel, 1947.
Jean Marguin, Histoire des instruments et machines à calculer, Hermann, 1994
Guy Mourlevat, Les machines arithmétiques de Blaise Pascal, La Française d’Édition et d’Imprimerie, Clermont-Ferrand, 1988
Jacques Moutaux dir., Pascal et la géométrie, Mont-Saint-Aignan, CRDP de Rouen : IREM de Rouen, 1993
Maurice d’Ocagne, Le Calcul simplifié, Gauthier-Villars et fils, 1893
Études d'œuvres particulières Pensées
Jean Mesnard, Les "Pensées" de Pascal, Paris, SEDES, 1976 troisième édition 1995
Marie Pérouse, L’Invention des Pensées de Pascal. Les éditions de Port-Royal 1670-1678, Champion, 2009.
Album jeunesse
Orietta Ombrosi, illustré par Géraldine Alibeu, Pascal, d'un infini à l'autre, coll. Coup de génie, éd. Seuil Jeunesse
Travaux de Blaise Pascal
Pari de Pascal
Triangle de Pascal
Théorème de Pascal
Ruban de Pascal
Sous le pseudonyme de Dettonville : le Traité de la roulette sur la méthode des indivisibles en géométrie
Pascaline (machine à calculer
Contemporains
Étienne Pascal, son père
Antoine Arnauld
Pierre de Fermat
Christian Huygens
Marin Mersenne
Références posthumes
Pascal, unité de mesure
Pascal langage
Université Blaise-Pascal à Clermont-Ferrand
Rue Pascal à Paris Paris 13e
Mathématiques en Europe au XVIIe siècle
Prix Blaise Pascal
En numismatique : 500 francs Pascal 1968-1993
    
Posté le : 18/06/2016 21:23
Edité par Loriane sur 19-06-2016 16:44:31
Edité par Loriane sur 19-06-2016 16:45:19
|
|
|
|
Mes préférences
Sont en ligne
45 Personne(s) en ligne ( 29 Personne(s) connectée(s) sur Les Forums)
Utilisateur(s): 0
Invité(s): 45
Plus ...
|
 Tous les messages
Tous les messages Tous les messages
Tous les messages